The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
DetailsMissing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
-
Examples
- References
Suppose the model contains s explanatory effects. For the jth observation, let 
be the estimated probability of the observed response. The three criteria displayed by the SURVEYLOGISTIC procedure are calculated
as follows:
-
–2 log likelihood:
![\[ -2\mbox{ Log L}=-2\sum _ j w_ j f_ j\log (\hat{\pi }_ j) \]](images/statug_surveylogistic0177.png)
where
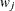and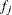 
are the weight and frequency values, respectively, of the jth observation. For binary response models that use the events/trials syntax, this is equivalent to
![\[ -2\mbox{ Log L}=-2\sum _ j w_ j f_ j \{ r_ j \log (\hat{\pi }_ j) + (n_ j-r_ j)\log (1-\hat{\pi }_ j) \} \]](images/statug_surveylogistic0178.png)
where
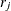is the number of events, 
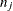is the number of trials, and 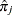is the estimated event probability.
-
Akaike information criterion:
![\[ \mbox{AIC}=-2\mbox{ Log L}+2p \]](images/statug_surveylogistic0181.png)
where p is the number of parameters in the model. For cumulative response models,
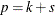, where k is the total number of response levels minus one, and s is the number of explanatory effects. For the generalized logit model, 
.
-
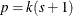Schwarz criterion:
![\[ \mbox{SC}=-2\mbox{ Log L}+p\log (\sum _ jf_ j) \]](images/statug_surveylogistic0184.png)
where p is the number of parameters in the model. For cumulative response models,
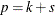, where k is the total number of response levels minus one, and s is the number of explanatory effects. For the generalized logit model, .
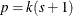The –2 log likelihood statistic has a chi-square distribution under the null hypothesis (that all the explanatory effects in the model are zero), and the procedure produces a p-value for this statistic. The AIC and SC statistics give two different ways of adjusting the –2 log likelihood statistic for the number of terms in the model and the number of observations used.