| Introduction |
There are a number of approaches to simulating a set of dependent random variables. In the context of spatial random fields, these include sequential indicator methods, turning bands, and the Karhunen-Loeve expansion. See Christakos (1992, Chapter 8) and Duetsch and Journel (1992, Chapter 5) for details.
In addition, there is the LU decomposition method, a particularly simple and computationally efficient for normal or Gaussian variates. For a given covariance matrix, the  decomposition is computed once, and the simulation proceeds by repeatedly generating a vector of independent
decomposition is computed once, and the simulation proceeds by repeatedly generating a vector of independent  random variables and multiplying by the
random variables and multiplying by the 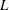 matrix.
matrix.
One problem with this technique is that memory is required to hold the covariance matrix of all the analysis and conditioning variables in core.