Estimability
Given a response or dependent variable 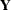 , predictors or independent variables
, predictors or independent variables 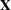 , and a linear expectation model
, and a linear expectation model 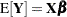 relating the two, a primary analytical goal is to estimate or test for the significance of certain linear combinations of the elements of
relating the two, a primary analytical goal is to estimate or test for the significance of certain linear combinations of the elements of 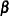 . For least squares regression and analysis of variance, this is accomplished by computing linear combinations of the observed
. For least squares regression and analysis of variance, this is accomplished by computing linear combinations of the observed 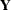 s. An unbiased linear estimate of a specific linear function of the individual
s. An unbiased linear estimate of a specific linear function of the individual  s, say
s, say  , is a linear combination of the
, is a linear combination of the 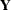 s that has an expected value of
s that has an expected value of  . Hence, the following definition:
. Hence, the following definition:
A linear combination of the parametersis estimable if and only if a linear combination of the
s exists that has expected value
.
Any linear combination of the 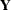 s, for instance
s, for instance 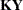 , will have expectation
, will have expectation 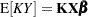 . Thus, the expected value of any linear combination of the
. Thus, the expected value of any linear combination of the 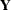 s is equal to that same linear combination of the rows of
s is equal to that same linear combination of the rows of 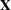 multiplied by
multiplied by 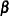 . Therefore,
. Therefore,
is estimable if and only if there is a linear combination of the rows of
that is equal to
—that is, if and only if there is a
such that
.
Thus, the rows of 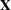 form a generating set from which any estimable
form a generating set from which any estimable 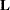 can be constructed. Since the row space of
can be constructed. Since the row space of 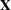 is the same as the row space of
is the same as the row space of  , the rows of
, the rows of  also form a generating set from which all estimable
also form a generating set from which all estimable 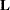 s can be constructed. Similarly, the rows of
s can be constructed. Similarly, the rows of  also form a generating set for
also form a generating set for 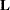 .
.
Therefore, if 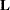 can be written as a linear combination of the rows of
can be written as a linear combination of the rows of 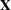 ,
,  , or
, or  , then
, then  is estimable.
is estimable.
In the context of least squares regression and analysis of variance, an estimable linear function 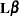 can be estimated by
can be estimated by 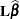 , where
, where  . From the general theory of linear models, the unbiased estimator
. From the general theory of linear models, the unbiased estimator 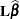 is, in fact, the best linear unbiased estimator of
is, in fact, the best linear unbiased estimator of 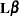 , in the sense of having minimum variance as well as maximum likelihood when the residuals are normal. To test the hypothesis that
, in the sense of having minimum variance as well as maximum likelihood when the residuals are normal. To test the hypothesis that 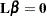 , compute the sum of squares
, compute the sum of squares
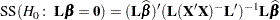 |
and form an  test with the appropriate error term. Note that in contexts more general than least squares regression (for example, generalized and/or mixed linear models), linear hypotheses are often tested by analogous sums of squares of the estimated linear parameters
test with the appropriate error term. Note that in contexts more general than least squares regression (for example, generalized and/or mixed linear models), linear hypotheses are often tested by analogous sums of squares of the estimated linear parameters  .
.