Estimate of Quantile

Let be the observed values for variable associated with sampling weights, where are the stratum index, cluster index, and member index, respectively, as shown in the section Definitions and Notation. Let denote the sample order statistics for variable .

An estimate of quantile is

where is the estimated cumulative distribution for :

and is the indicator function.

Standard Error

PROC SURVEYMEANS  uses Woodruff’s method (Dorfman and Valliant 1993; Särndal, Swensson, and Wretman 1992; and Francisco and Fuller 1991) to estimate the variances of quantiles. This method first constructs a confidence interval on a quantile. Then it uses the width of the confidence interval to estimate the standard error of a quantile.

In order to estimate the variance for , first the procedure estimates the variance of the estimated distribution function by

where

Then % confidence limits of can be constructed by

where 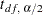is the 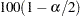th percentile of the t distribution with df degrees of freedom, described in the section Degrees of Freedom.

When is out of the range of [0,1], the procedure does not compute the standard error.

The th quantile is defined as

and the th quantile is defined as

The standard error of then is estimated by

where 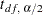is the 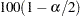th percentile of the t distribution with df degrees of freedom.

Confidence Limits

Symmetric % confidence limits are computed as

If you specify the NONSYMCL option in the SURVEYMEANS  statement, the procedure computes % nonsymmetric confidence limits: