| The SURVEYLOGISTIC Procedure |
Jackknife Method
The jackknife method of variance estimation deletes one PSU at a time from the full sample to create replicates. The total number of replicates 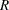 is the same as the total number of PSUs. In each replicate, the sample weights of the remaining PSUs are modified by the jackknife coefficient
is the same as the total number of PSUs. In each replicate, the sample weights of the remaining PSUs are modified by the jackknife coefficient 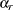 . The modified weights are called replicate weights.
. The modified weights are called replicate weights.
The jackknife coefficient and replicate weights are described as follows.
Without Stratification
If there is no stratification in the sample design (no STRATA statement), the jackknife coefficients 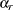 are the same for all replicates:
are the same for all replicates:
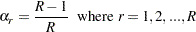 |
Denote the original weight in the full sample for the 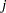 th member of the
th member of the  th PSU as
th PSU as 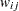 . If the
. If the  th PSU is included in the
th PSU is included in the  th replicate (
th replicate (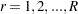 ), then the corresponding replicate weight for the
), then the corresponding replicate weight for the 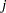 th member of the
th member of the  th PSU is defined as
th PSU is defined as
 |
With Stratification
If the sample design involves stratification, each stratum must have at least two PSUs to use the jackknife method.
Let stratum 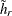 be the stratum from which a PSU is deleted for the
be the stratum from which a PSU is deleted for the  th replicate. Stratum
th replicate. Stratum 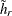 is called the donor stratum. Let
is called the donor stratum. Let 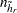 be the total number of PSUs in the donor stratum
be the total number of PSUs in the donor stratum 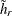 . The jackknife coefficients are defined as
. The jackknife coefficients are defined as
 |
Denote the original weight in the full sample for the 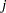 th member of the
th member of the  th PSU as
th PSU as 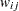 . If the
. If the  th PSU is included in the
th PSU is included in the  th replicate (
th replicate (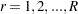 ), then the corresponding replicate weight for the
), then the corresponding replicate weight for the 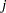 th member of the
th member of the  th PSU is defined as
th PSU is defined as
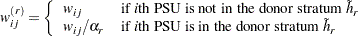 |
You can use the VARMETHOD=JACKKNIFE(OUTJKCOEFS=) method-option to save the jackknife coefficients into a SAS data set and use the VARMETHOD=JACKKNIFE(OUTWEIGHTS=) method-option to save the replicate weights into a SAS data set.
If you provide your own replicate weights with a REPWEIGHTS statement, then you can also provide corresponding jackknife coefficients with the JKCOEFS= option.
Let  be the estimated regression coefficients from the full sample for
be the estimated regression coefficients from the full sample for 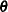 . Let
. Let  be the estimated regression coefficient obtained from the
be the estimated regression coefficient obtained from the  th replicate by using replicate weights. PROC SURVEYLOGISTIC estimates the covariance matrix of
th replicate by using replicate weights. PROC SURVEYLOGISTIC estimates the covariance matrix of  by
by
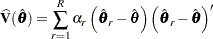 |
with 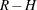 degrees of freedom, where
degrees of freedom, where 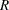 is the number of replicates and
is the number of replicates and  is the number of strata, or
is the number of strata, or 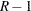 when there is no stratification.
when there is no stratification.
Copyright © SAS Institute, Inc. All Rights Reserved.