| The SURVEYLOGISTIC Procedure |
Logistic Regression Models
If the response categories of the response variable 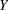 can be restricted to a number of ordinal values, you can fit cumulative probabilities of the response categories with a cumulative logit model, a complementary log-log model, or a probit model. Details of cumulative logit models (or proportional odds models) can be found in McCullagh and Nelder (1989). If the response categories of
can be restricted to a number of ordinal values, you can fit cumulative probabilities of the response categories with a cumulative logit model, a complementary log-log model, or a probit model. Details of cumulative logit models (or proportional odds models) can be found in McCullagh and Nelder (1989). If the response categories of 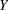 are nominal responses without natural ordering, you can fit the response probabilities with a generalized logit model. Formulation of the generalized logit models for nominal response variables can be found in Agresti (2002). For each model, the procedure estimates the model parameter
are nominal responses without natural ordering, you can fit the response probabilities with a generalized logit model. Formulation of the generalized logit models for nominal response variables can be found in Agresti (2002). For each model, the procedure estimates the model parameter 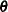 by using a pseudo-log-likelihood function. The procedure obtains the pseudo-maximum likelihood estimator
by using a pseudo-log-likelihood function. The procedure obtains the pseudo-maximum likelihood estimator 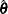 by using iterations described in the section Iterative Algorithms for Model Fitting and estimates its variance described in the section Variance Estimation.
by using iterations described in the section Iterative Algorithms for Model Fitting and estimates its variance described in the section Variance Estimation.
Cumulative Logit Model
A cumulative logit model uses the logit function
 |
as the link function.
Denote the cumulative sum of the expected proportions for the first  categories of variable
categories of variable 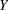 by
by
 |
for  Then the cumulative logit model can be written as
Then the cumulative logit model can be written as
 |
with the model parameters
 |
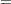 |
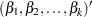 |
|||
 |
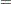 |
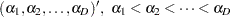 |
|||
 |
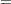 |
 |
Complementary Log-Log Model
A complementary log-log model uses the complementary log-log function
 |
as the link function. Denote the cumulative sum of the expected proportions for the first  categories of variable
categories of variable 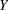 by
by
 |
for  Then the complementary log-log model can be written as
Then the complementary log-log model can be written as
 |
with the model parameters
 |
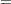 |
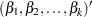 |
|||
 |
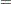 |
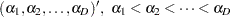 |
|||
 |
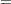 |
 |
Probit Model
A probit model uses the probit (or normit) function, which is the inverse of the cumulative standard normal distribution function,
 |
as the link function, where
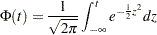 |
Denote the cumulative sum of the expected proportions for the first  categories of variable
categories of variable 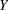 by
by
 |
for  Then the probit model can be written as
Then the probit model can be written as
 |
with the model parameters
 |
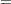 |
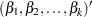 |
|||
 |
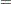 |
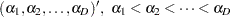 |
|||
 |
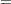 |
 |
Generalized Logit Model
For nominal response, a generalized logit model is to fit the ratio of the expected proportion for each response category over the expected proportion of a reference category with a logit link function.
Without loss of generality, let category 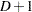 be the reference category for the response variable
be the reference category for the response variable 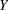 . Denote the expected proportion for the
. Denote the expected proportion for the  th category by
th category by 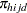 as in the section Notation. Then the generalized logit model can be written as
as in the section Notation. Then the generalized logit model can be written as
 |
for  with the model parameters
with the model parameters
 |
 |
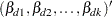 |
|||
 |
 |
 |
Copyright © SAS Institute, Inc. All Rights Reserved.