| The STEPDISC Procedure |
| Displayed Output |
The displayed output from PROC STEPDISC includes the class level information table. For each level of the classification variable, the following information is provided: the output data set variable name, frequency sum, weight sum, and the proportion of the total sample.
The optional output from PROC STEPDISC includes the following:
The optional output includes the following:
Within-class SSCP matrices for each group
Pooled within-class SSCP matrix
Between-class SSCP matrix
Total-sample SSCP matrix
Within-class covariance matrices for each group
Pooled within-class covariance matrix
Between-class covariance matrix, equal to the between-class SSCP matrix divided by
 , where
, where  is the number of observations and
is the number of observations and  is the number of classes
is the number of classes Total-sample covariance matrix
Within-class correlation coefficients and
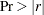 to test the hypothesis that the within-class population correlation coefficients are zero
to test the hypothesis that the within-class population correlation coefficients are zero Pooled within-class correlation coefficients and
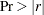 to test the hypothesis that the partial population correlation coefficients are zero
to test the hypothesis that the partial population correlation coefficients are zero Between-class correlation coefficients and
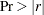 to test the hypothesis that the between-class population correlation coefficients are zero
to test the hypothesis that the between-class population correlation coefficients are zero Total-sample correlation coefficients and
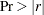 to test the hypothesis that the total population correlation coefficients are zero
to test the hypothesis that the total population correlation coefficients are zero Simple statistics, including
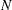 (the number of observations), sum, mean, variance, and standard deviation for the total sample and within each class
(the number of observations), sum, mean, variance, and standard deviation for the total sample and within each class Total-sample standardized class means, obtained by subtracting the grand mean from each class mean and dividing by the total-sample standard deviation
Pooled within-class standardized class means, obtained by subtracting the grand mean from each class mean and dividing by the pooled within-class standard deviation
At each step, the following statistics are displayed:
for each variable considered for entry or removal: partial R-square, the squared (partial) correlation, the
 statistic, and
statistic, and 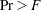 , the probability level, from a one-way analysis of covariance
, the probability level, from a one-way analysis of covariance the minimum tolerance for entering each variable. A variable is entered only if its tolerance and the tolerances for all variables already in the model are greater than the value specified in the SINGULAR= option. The tolerance for the entering variable is
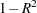 from regressing the entering variable on the other variables already in the model. The tolerance for a variable already in the model is
from regressing the entering variable on the other variables already in the model. The tolerance for a variable already in the model is 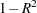 from regressing that variable on the entering variable and the other variables already in the model. With
from regressing that variable on the entering variable and the other variables already in the model. With  variables already in the model, for each entering variable,
variables already in the model, for each entering variable, 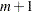 multiple regressions are performed by using the entering variable and each of the
multiple regressions are performed by using the entering variable and each of the  variables already in the model as a dependent variable. These
variables already in the model as a dependent variable. These 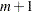 tolerances are computed for each entering variable, and the minimum tolerance is displayed for each.
tolerances are computed for each entering variable, and the minimum tolerance is displayed for each. The tolerance is computed by using the total-sample correlation matrix. It is customary to compute tolerance by using the pooled within-class correlation matrix (Jennrich; 1977), but it is possible for a variable with excellent discriminatory power to have a high total-sample tolerance and a low pooled within-class tolerance. For example, PROC STEPDISC enters a variable that yields perfect discrimination (that is, produces a canonical correlation of one), but a program that uses pooled within-class tolerance does not.
the variable label, if any
the name of the variable chosen
the variables already selected or removed
Wilks’ lambda and the associated
 approximation with degrees of freedom and
approximation with degrees of freedom and 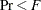 , the associated probability level after the selected variable has been entered or removed. Wilks’ lambda is the likelihood ratio statistic for testing the hypothesis that the means of the classes on the selected variables are equal in the population (see the section Multivariate Tests in
Chapter 4,
Introduction to Regression Procedures.
) Lambda is close to zero if any two groups are well separated.
, the associated probability level after the selected variable has been entered or removed. Wilks’ lambda is the likelihood ratio statistic for testing the hypothesis that the means of the classes on the selected variables are equal in the population (see the section Multivariate Tests in
Chapter 4,
Introduction to Regression Procedures.
) Lambda is close to zero if any two groups are well separated. Pillai’s trace and the associated
 approximation with degrees of freedom and
approximation with degrees of freedom and 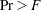 , the associated probability level after the selected variable has been entered or removed. Pillai’s trace is a multivariate statistic for testing the hypothesis that the means of the classes on the selected variables are equal in the population (see the section Multivariate Tests in
Chapter 4,
Introduction to Regression Procedures
).
, the associated probability level after the selected variable has been entered or removed. Pillai’s trace is a multivariate statistic for testing the hypothesis that the means of the classes on the selected variables are equal in the population (see the section Multivariate Tests in
Chapter 4,
Introduction to Regression Procedures
). Average squared canonical correlation (ASCC). The ASCC is Pillai’s trace divided by the number of groups minus 1. The ASCC is close to 1 if all groups are well separated and if all or most directions in the discriminant space show good separation for at least two groups.
Summary to give statistics associated with the variable chosen at each step. The summary includes the following:
Step number
Variable entered or removed
Number in, the number of variables in the model
Partial R-square
the
 value for entering or removing the variable
value for entering or removing the variable 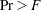 , the probability level for the
, the probability level for the  statistic
statistic Wilks’ lambda
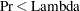 based on the
based on the  approximation to Wilks’ lambda
approximation to Wilks’ lambda Average squared canonical correlation
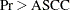 based on the
based on the  approximation to Pillai’s trace
approximation to Pillai’s trace the variable label, if any
Copyright © SAS Institute, Inc. All Rights Reserved.