For a conditional simulation, this distribution of

must be conditioned on the values of the CONDITION variables. The relevant general result concerning conditional distributions of multivariate normal random variables is the following. Let , where

and where is , is , is , is , and is , with . The full vector has simply been partitioned into two subvectors, and , and has been similarly partitioned into covariances and cross covariances.

With this notation, the distribution of conditioned on is , with

and

See Searle (1971, pp. 46–47) for details.

Using the SIMNORMAL procedure corresponds with the conditional simulation as follows. Let be the VAR variables as before (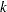 is the number of variables in the VAR list). Let the mean vector for be denoted by . Let the CONDITION variables be denoted by (where is the number of variables in the COND list). Let the mean vector for be denoted by and the conditioning values be denoted by

Then stacking

the variance of is

where , , and . By using the preceding general result, the relevant covariance matrix is

and the mean is

By using and , simulating now proceeds as in the unconditional case.