Three tests are available in the QUANTREG procedure for the linear null hypothesis 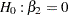 . Here
. Here 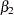 denotes a subset of the parameters, where the parameter vector
denotes a subset of the parameters, where the parameter vector 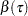 is partitioned as
is partitioned as 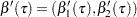 , and the covariance matrix
, and the covariance matrix 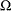 for the parameter estimates is partitioned correspondingly as
for the parameter estimates is partitioned correspondingly as  with
with 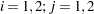 ; and
; and 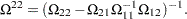
The Wald test statistic, which is based on the estimated coefficients for the unrestricted model, is given by
where 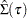 is an estimator of the covariance of
is an estimator of the covariance of 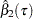 . The QUANTREG procedure provides two estimators for the covariance, as described in the previous section. The estimator based on the asymptotic covariance is
. The QUANTREG procedure provides two estimators for the covariance, as described in the previous section. The estimator based on the asymptotic covariance is
where 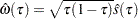 and
and  is the estimated sparsity function. The estimator based on the bootstrap covariance is the empirical covariance of the MCMB samples.
is the estimated sparsity function. The estimator based on the bootstrap covariance is the empirical covariance of the MCMB samples.
The likelihood ratio test is based on the difference between the objective function values in the restricted and unrestricted models. Let 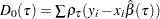 and
and 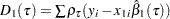 , and set
, and set
where  is the estimated sparsity function.
is the estimated sparsity function.
The rank test statistic under iid error models is given by
where
and 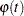 is a score function. The following three score functions are available in the QUANTREG procedure:
is a score function. The following three score functions are available in the QUANTREG procedure:
- Wilcoxon scores:

- normal scores:
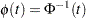 , where
, where  is the normal distribution function
is the normal distribution function
- sign scores:
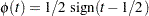
An important feature of the rank test statistic 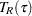 is that, unlike Wald tests or likelihood ratio tests, no estimation of the sparsity function
is that, unlike Wald tests or likelihood ratio tests, no estimation of the sparsity function 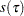 is required.
is required.
Koenker and Machado (1999) prove that the three test statistics ( 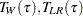 , and
, and 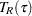 ) are asymptotically equivalent and that their distributions converge to
) are asymptotically equivalent and that their distributions converge to 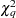 under the null hypothesis, where
under the null hypothesis, where 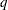 is the dimension of
is the dimension of 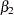 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.
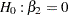 . Here
. Here 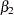 denotes a subset of the parameters, where the parameter vector
denotes a subset of the parameters, where the parameter vector 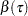 is partitioned as
is partitioned as 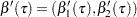 , and the covariance matrix
, and the covariance matrix 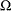 for the parameter estimates is partitioned correspondingly as
for the parameter estimates is partitioned correspondingly as  with
with 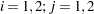 ; and
; and 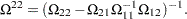
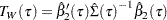
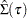 is an estimator of the covariance of
is an estimator of the covariance of 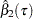 . The QUANTREG procedure provides two estimators for the covariance, as described in the previous section. The estimator based on the asymptotic covariance is
. The QUANTREG procedure provides two estimators for the covariance, as described in the previous section. The estimator based on the asymptotic covariance is 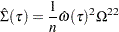
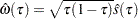 and
and  is the estimated sparsity function. The estimator based on the bootstrap covariance is the empirical covariance of the MCMB samples.
is the estimated sparsity function. The estimator based on the bootstrap covariance is the empirical covariance of the MCMB samples. 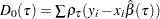 and
and 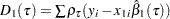 , and set
, and set 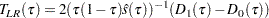
 is the estimated sparsity function.
is the estimated sparsity function. 


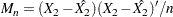


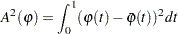

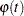 is a score function. The following three score functions are available in the QUANTREG procedure:
is a score function. The following three score functions are available in the QUANTREG procedure: 
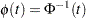 , where
, where  is the normal distribution function
is the normal distribution function 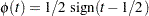
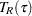 is that, unlike Wald tests or likelihood ratio tests, no estimation of the sparsity function
is that, unlike Wald tests or likelihood ratio tests, no estimation of the sparsity function 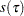 is required.
is required. 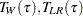 , and
, and 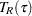 ) are asymptotically equivalent and that their distributions converge to
) are asymptotically equivalent and that their distributions converge to 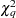 under the null hypothesis, where
under the null hypothesis, where 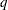 is the dimension of
is the dimension of 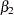 .
.