| The QUANTREG Procedure |
| Quantile Regression |
Quantile regression generalizes the concept of a univariate quantile to a conditional quantile given one or more covariates. Recall that a student’s score on a test is at the  th quantile if his or her score is better than that of
th quantile if his or her score is better than that of  of the students who took the test. The score is also said to be at the 100
of the students who took the test. The score is also said to be at the 100 th percentile.
th percentile.
For a random variable 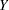 with probability distribution function
with probability distribution function
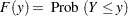 |
the  th quantile of
th quantile of 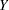 is defined as the inverse function
is defined as the inverse function
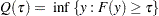 |
where 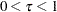 . In particular, the median is
. In particular, the median is 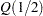 .
.
For a random sample 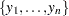 of
of 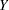 , it is well known that the sample median minimizes the sum of absolute deviations
, it is well known that the sample median minimizes the sum of absolute deviations
 |
Likewise, the general  th sample quantile
th sample quantile 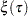 , which is the analog of
, which is the analog of 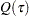 , is formulated as the minimizer
, is formulated as the minimizer
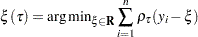 |
where 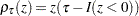 ,
, 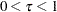 , and where
, and where 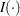 denotes the indicator function. The loss function
denotes the indicator function. The loss function  assigns a weight of
assigns a weight of  to positive residuals
to positive residuals 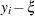 and a weight of
and a weight of 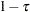 to negative residuals.
to negative residuals.
Using this loss function, the linear conditional quantile function extends the  th sample quantile
th sample quantile 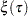 to the regression setting in the same way that the linear conditional mean function extends the sample mean. Recall that OLS regression estimates the linear conditional mean function
to the regression setting in the same way that the linear conditional mean function extends the sample mean. Recall that OLS regression estimates the linear conditional mean function  by solving for
by solving for
 |
The estimated parameter 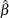 minimizes the sum of squared residuals in the same way that the sample mean
minimizes the sum of squared residuals in the same way that the sample mean 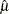 minimizes the sum of squares:
minimizes the sum of squares:
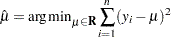 |
Likewise, quantile regression estimates the linear conditional quantile function, 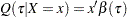 , by solving
, by solving
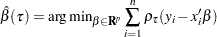 |
for  . The quantity
. The quantity 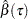 is called the
is called the  th regression quantile. The case
th regression quantile. The case 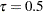 , which minimizes the sum of absolute residuals, corresponds to median regression, which is also known as
, which minimizes the sum of absolute residuals, corresponds to median regression, which is also known as 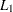 regression.
regression.
The set of regression quantiles
 |
is referred to as the quantile process.
The QUANTREG procedure computes the quantile function  and conducts statistical inference on the estimated parameters
and conducts statistical inference on the estimated parameters 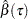 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.