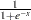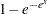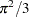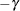PROC PROBIT: Distributions :: SAS/STAT(R) 9.22 User's Guide

The PROBIT Procedure

Distributions

The distributions, $\text{[math]}$ , allowed in the PROBIT procedure are specified with the DISTRIBUTION= option in the MODEL statement. The cumulative distribution functions for the available distributions are

Cumulative Distribution Function	Distribution
$\text{[math]}$	Normal
$\text{[math]}$	Logistic
$\text{[math]}$	Extreme value or Gompertz

The variances of these three distributions are not all equal to 1, and their means are not all equal to zero. Their means and variances are shown in the following table, where 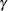$\text{[math]}$ is the Euler constant.

Distribution	Mean	Variance
Normal	0	1
Logistic	0	$\text{[math]}$
Extreme value or Gompertz	$\text{[math]}$	$\text{[math]}$

When comparing parameter estimates by using different distributions, you need to take into account the different scalings and, for the extreme value (or Gompertz) distribution, a possible shift in location. For example, if the fitted probabilities are in the neighborhood of 0.1 to 0.9, then the parameter estimates from the logistic model should be about 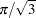$\text{[math]}$ larger than the estimates from the probit model.

Top of Page