PROC PHREG: Input and Output Data Sets :: SAS/STAT(R) 9.22 User's Guide

The PHREG Procedure

Input and Output Data Sets

OUTEST= Output Data Set

The OUTEST= data set contains one observation for each BY group containing the maximum likelihood estimates of the regression coefficients. If you also use the COVOUT option in the PROC PHREG statement, there are additional observations containing the rows of the estimated covariance matrix. If you specify SELECTION=FORWARD, BACKWARD, or STEPWISE, only the estimates of the parameters and covariance matrix for the final model are output to the OUTEST= data set.

Variables in the OUTEST= Data Set

The OUTEST= data set contains the following variables:

any BY variables specified
_TIES_, a character variable of length 8 with four possible values: BRESLOW, DISCRETE, EFRON, and EXACT. These are the four values of the TIES= option in the MODEL statement.
_TYPE_, a character variable of length 8 with two possible values: PARMS for parameter estimates or COV for covariance estimates. If both the COVM and COVS options are specified in the PROC PHREG statement along with the COVOUT option, _TYPE_=’COVM’ for the model-based covariance estimates and _TYPE_=’COVS’ for the robust sandwich covariance estimates.
_STATUS_, a character variable indicating whether the estimates have converged
_NAME_, a character variable containing the name of the TIME variable for the row of parameter estimates and the name of each explanatory variable to label the rows of covariance estimates
one variable for each regression coefficient and one variable for the offset variable if the OFFSET= option is specified. If an explanatory variable is not included in the final model in a variable selection process, the corresponding parameter estimates and covariances are set to missing.
_LNLIKE_, a numeric variable containing the last computed value of the log likelihood

Parameter Names in the OUTEST= Data Set

For continuous explanatory variables, the names of the parameters are the same as the corresponding variables. For CLASS variables, the parameter names are obtained by concatenating the corresponding CLASS variable name with the CLASS category; see the PARAM= option in the CLASS statement for more details. For interaction and nested effects, the parameter names are created by concatenating the names of each component effect.

INEST= Input Data Set

You can specify starting values for the maximum likelihood iterative algorithm in the INEST= data set. The INEST= data set has the same structure as the OUTEST= data set but is not required to have all the variables or observations that appear in the OUTEST= data set.

The INEST= data set must contain variables that represent the regression coefficients of the model. If BY processing is used, the INEST= data set should also include the BY variables, and there must be one observation for each BY group. If the INEST= data set also contains the _TYPE_ variable, only observations with _TYPE_ value ’PARMS’ are used as starting values.

OUT= Output Data Set in the OUTPUT Statement

The OUT= data set in the OUTPUT statement contains all the variables in the input data set, along with statistics you request by specifying keyword=name options. The new variables contain a variety of diagnostics that are calculated for each observation in the input data set.

OUT= Output Data Set in the BASELINE Statement

The OUT= data set in the BASELINE statement contains all the variables in the COVARIATES= data set, along with statistics you request by specifying keyword=name options. For unstratified input data, there are 1+ $\text{[math]}$ observations in the OUT= data set for each observation in the COVARIATES= data set, where $\text{[math]}$ is the number of distinct event times in the input data. 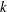For input data that are stratified into $\text{[math]}$ strata, with $\text{[math]}$ distinct events in the $\text{[math]}$ th stratum, 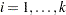$\text{[math]}$ , there are 1+ $\text{[math]}$ observations for the $\text{[math]}$ th stratum in the OUT= data set for each observation in the COVARIATES= data set.

OUTPOST= Output Data Set in the BAYES Statement

The OUTPOST= data set contains the generated posterior samples. There are 3+ $\text{[math]}$ variables, where $\text{[math]}$ is the number of model parameters. The variable Iteration represents the iteration number, the variable LogLike contains the log-likelihood values, and the variable LogPost contains the log-posterior-density values. The other $\text{[math]}$ variables represent the draws of the Markov chain for the model parameters.

Top of Page