If you specify the ANOVA option, PROC NPAR1WAY displays a "Class Means" table and an "Analysis of Variance" table for each response variable. The "Class Means" table includes the following information for each CLASS variable value or level:

• N, the number of observations

• Mean of the response variable

The "Analysis of Variance" table includes the following information for each Source of variation (Among classes, and Within classes):

• DF, the degrees of freedom associated with the source

• Sum of Squares

• Mean Square, the sum of squares divided by the degrees of freedom

The "Analysis of Variance" table also includes the following:

• F Value for testing the hypothesis that the group means are equal. This is computed by dividing the Mean Square (Among) by the Mean Square (Within).

• Pr > F, the significance probability corresponding to the F Value

For each score type that you specify, PROC NPAR1WAY displays a "Class Scores" table. The available score types include Wilcoxon, median, Van der Waerden (normal), Savage, Siegel-Tukey, Ansari-Bradley, Klotz, Mood, Conover, and raw data scores. PROC NPAR1WAY computes the scores for the response variable values, and classifies the scored observations according to the CLASS variable values. The "Class Scores" table includes the following information for each CLASS variable level:

• N, the number of observations

• Sum of Scores

• Expected Under H0, the expected sum of scores under the null hypothesis of no difference among classes

• Std Dev Under H0, the standard deviation under the null hypothesis

• Mean Score

When there are only two levels of the CLASS variable, PROC NPAR1WAY displays the following "Two-Sample Test" results for each analysis of scores:

• Statistic, which is the sum of scores for the class with the smaller sample size

• Z, the standardized test statistic, which has an asymptotic standard normal distribution under the null hypothesis

• One-Sided Pr < Z, or One-Sided Pr > Z, the asymptotic one-sided p-value, which is displayed as Pr < Z or Pr > Z, depending on whether Z is 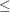0 or > 0

• Two-Sided Pr > |Z|, the asymptotic two-sided 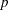-value

For Wilcoxon scores, PROC NPAR1WAY also displays a t-approximation for the two-sample test.

If you request an exact test by specifying the score type in the EXACT statement, PROC NPAR1WAY displays the following exact p-values for two-sample data:

• One-Sided Pr 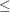S, or One-Sided Pr S, the exact one-sided p-value, which is displayed as Pr 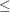S or Pr S, depending on whether S 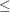Mean or S > Mean, where S is the test statistic and Mean is its expected value under the null hypothesis

• Point Pr = S, the point probability, if you specify the POINT option in the EXACT statement

• Two-Sided Pr |S - Mean|, the exact two-sided p-value

If you request Monte Carlo estimates for the exact test by specifying the MC option in the EXACT statement, PROC NPAR1WAY displays the following information for two-sample data:

• Estimate of One-Sided Pr 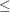S or One-Sided Pr S, the exact one-sided p-value, together with its Lower and Upper Confidence Limits

• Estimate of Two-Sided Pr |S - Mean|, the exact two-sided p-value, together with its Lower and Upper Confidence Limits

• Number of Samples used to compute the Monte Carlo estimates

• Initial Seed used to compute the Monte Carlo estimates

For both two-sample and multisample data, PROC NPAR1WAY displays the following "One-Way Analysis" for each score type:

• Chi-Square, the one-way ANOVA statistic for testing the null hypothesis of no difference among classes

• DF, the degrees of freedom

• Pr > Chi-Square, the asymptotic 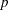-value

For multisample data, if you request an exact test by specifying the score type in the EXACT statement, PROC NPAR1WAY also displays the exact 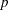-value as follows:

• Exact Pr Chi-Square

• Exact Pr = Chi-Square, the point probability, if you specify the POINT option in the EXACT statement

For multisample data, if you request a Monte Carlo estimate for the exact test by specifying the MC option in the EXACT statement, PROC NPAR1WAY displays the following information:

• Estimate of Exact Pr Chi-Square, together with its Lower and Upper Confidence Limits

• Number of Samples used to compute the Monte Carlo estimate

• Initial Seed used to compute the Monte Carlo estimate

If you specify the HL option, PROC NPAR1WAY produces a "Hodges-Lehmann Estimation" table for two-sample data, which includes the following information:

• Location Shift estimate

• Confidence Limits for the Location Shift

• Confidence Interval Midpoint

• Asymptotic Standard Error estimate, based on the confidence interval

If you request exact Hodges-Lehmann confidence limits by specifying the HL option in the EXACT statement, the "Hodges-Lehmann Estimation" table also includes Exact Confidence Limits and the exact Interval Midpoint.

If you specify the EDF option, PROC NPAR1WAY produces tables for the Kolmogorov-Smirnov Test, the Cramer-von Mises Test, and for two-sample data only, the Kuiper Test.

The "Kolmogorov-Smirnov Test" table includes the following information for each CLASS variable level:

• N, the number of observations

• EDF at Maximum, the value of the class EDF (empirical distribution function) at its maximum deviation from the pooled EDF

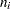• Deviation from Mean at Maximum, the value of at its maximum, where is the class sample size, is the class EDF, and 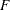is the pooled EDF

PROC NPAR1WAY displays the following Kolmogorov-Smirnov statistics:

• KS, the Kolmogorov-Smirnov statistic

• KSa, the asymptotic Kolmogorov-Smirnov statistic, where KSa = KS

For two-sample data, PROC NPAR1WAY displays the following Kolmogorov-Smirnov statistics:

• Pr > KSa, the asymptotic p-value for KSa, which equals Pr > D

• D, the two-sample Kolmogorov-Smirnov statistic, which is

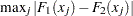
For two-sample data, if you specify the D option, PROC NPAR1WAY also displays the following one-sided Kolmogorov-Smirnov statistics and their asymptotic p-values:

• D+, which is

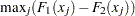
• Pr > D+

• D-, which is

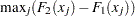
• Pr > D-

For two-sample data, if you request an exact Kolmogorov-Smirnov test by specifying the KS option in the EXACT statement, PROC NPAR1WAY displays the following exact p-values:

• Exact Pr D

• Exact Pr D+

• Exact Pr D-

• Exact Point Pr = D, Exact Point Pr = D+, and Exact Point Pr = D-, if you specify the POINT option in the EXACT statement

If you request Monte Carlo estimates for the two-sample exact Kolmogorov-Smirnov test, PROC NPAR1WAY displays the following information for two-sample data:

• Estimate of Exact Pr D, together with its Lower and Upper Confidence Limits

• Estimate of Exact Pr D+, together with its Lower and Upper Confidence Limits

• Estimate of Exact Pr D-, together with its Lower and Upper Confidence Limits

• Number of Samples used to compute the Monte Carlo estimates

• Initial Seed used to compute the Monte Carlo estimates

The "Cramer-von Mises Test" table includes the following information for each CLASS variable level:

• N, the number of observations

• Summed Deviation from Mean, which is

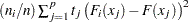
PROC NPAR1WAY also displays the following Cramer-von Mises statistics:

• CM, the Cramer-von Mises statistic

• CMa, the asymptotic Cramer-von Mises statistic, where CMa = CM

For two-sample data, PROC NPAR1WAY displays the "Kuiper Test" table, which includes the following information for each CLASS variable level:

• N, the number of observations

• Deviation from Mean, which is

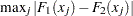
PROC NPAR1WAY also displays the following Kuiper two-sample test statistics:

• K, the Kuiper two-sample test statistic

• Ka, the asymptotic Kuiper two-sample test statistic, where Ka = K

• Pr > Ka