Overview: MI Procedure

The MI procedure performs multiple imputation of missing data. Missing values are an issue in a substantial number of statistical analyses. Most SAS statistical procedures exclude observations with any missing variable values from the analysis. These observations are called incomplete cases. Although analyzing only complete cases has the advantage of simplicity, the information contained in the incomplete cases is lost. This approach also ignores possible systematic differences between the complete cases and the incomplete cases, and the resulting inference might not be applicable to the population of all cases, especially with a small number of complete cases.

Some SAS procedures use all the available cases in an analysis—that is, cases with useful information. For example, the CORR procedure estimates a variable mean by using all cases with nonmissing values for this variable, ignoring the possible missing values in other variables. PROC CORR also estimates a correlation by using all cases with nonmissing values for this pair of variables. This makes better use of the available data than using only the complete cases does, but the resulting correlation matrix might not be positive definite.

Another strategy for handling missing data is single imputation, which substitutes a value for each missing value. Standard statistical procedures for complete data analysis can then be used with the filled-in data set. For example, each missing value can be imputed with the variable mean of the complete cases, or it can be imputed with the mean conditional on observed values of other variables. This approach treats missing values as if they were known in the complete-data analysis. However, single imputation does not reflect the uncertainty about the predictions of the unknown missing values, and the resulting estimated variances of the parameter estimates will be biased toward zero (Rubin 1987, p. 13).

Instead of filling in a single value for each missing value, multiple imputation (Rubin 1976, 1987) replaces each missing value with a set of plausible values that represent the uncertainty about the right value to impute. The multiply imputed data sets are then analyzed by using standard procedures for complete data and combining the results from these analyses. No matter which complete-data analysis is used, the process of combining results from different data sets is essentially the same.

Multiple imputation does not attempt to estimate each missing value through simulated values. Instead, it draws a random sample of the missing values from its distribution. This process results in valid statistical inferences that properly reflect the uncertainty due to missing values—for example, confidence intervals with the correct probability coverage.

Multiple imputation inference involves three distinct phases:

1. The missing data are filled in m times to generate m complete data sets.

2. The m complete data sets are analyzed using standard statistical analyses.

3. The results from the m complete data sets are combined to produce inferential results.

The MI procedure creates multiply imputed data sets for incomplete multivariate data. It uses methods that incorporate appropriate variability across the m imputations. The method of choice depends on the patterns of missingness.

A data set with variables 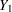, , 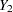..., 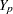(in that order) is said to have a monotone missing pattern when the event that a variable 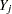is missing for a particular individual implies that all subsequent variables 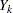, , 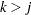are missing for that individual.

For data sets with monotone missing patterns, either a parametric method that assumes multivariate normality or a nonparametric method is appropriate to impute missing values for a continuous variable. Parametric methods available include the regression method (Rubin 1987, pp. 166–167) and the predictive mean matching method (Heitjan and Little 1991; Schenker and Taylor 1996). The nonparametric method is the propensity score method (Rubin 1987, pp. 124, 158).

To impute missing values for a classification variable in data sets with monotone missing patterns, you can use the logistic regression method when the classification variable has a binary or ordinal response, and the discriminant function method when the classification variable has a binary or nominal response.

For data sets with arbitrary missing patterns, a Markov chain Monte Carlo (MCMC) method (Schafer 1997) that assumes multivariate normality is used to impute all missing values or just enough missing values for continuous variables to make the imputed data sets have monotone missing patterns. When an imputed data set has a monotone missing pattern, methods for data sets with monotone missing patterns can then be used to impute remaining missing values.

Once the m complete data sets are analyzed using standard SAS procedures, the MIANALYZE procedure can be used to generate valid statistical inferences about these parameters by combining results from the m analyses.

Often, as few as three to five imputations are adequate in multiple imputation (Rubin 1996, p. 480). The relative efficiency of the small imputation estimator is high for cases with little missing information (Rubin 1987, p. 114). (Also see the section Multiple Imputation Efficiency.)

Multiple imputation inference assumes that the model (variables) you used to analyze the multiply imputed data (the analyst’s model) is the same as the model used to impute missing values in multiple imputation (the imputer’s model). But in practice, the two models might not be the same. The consequences for different scenarios (Schafer 1997, pp. 139–143) are discussed in the section Imputer’s Model Versus Analyst’s Model.

When an MCMC method is used to used to impute missing values, the trace (time series) and autocorrelation function plots for parameters such as variable means and covariances can be displayed to check for convergence of the MCMC method. See the section Checking Convergence in MCMC for a detailed description of these plots. If the ODS GRAPHICS ON statement is specified, these statistical graphics are created via the Output Delivery System (ODS). Otherwise, the traditional graphics are created.