The loess algorithm to obtain a predicted value at a given point in the predictor space proceeds by doing a least squares fit that uses all data points close to the given point. Thus the algorithm depends critically on the metric used to define closeness. This has the consequence that if you have more than one predictor variable and these predictor variables have significantly different scales, then closeness depends almost entirely on the variable with the largest scaling. It also means that merely changing the units of one of your predictors can significantly change the loess model fit.

To circumvent this problem, it is necessary to standardize the scale of the independent variables in the loess model. The SCALE= option in the MODEL statement is provided for this purpose. PROC LOESS uses a symmetrically trimmed standard deviation as the scale estimate for each independent variable of the loess model. This is a robust scale estimator in that extreme values of a variable are discarded before estimating the data scaling. For example, to compute a 10% trimmed standard deviation of a sample, you discard the smallest and largest 5% of the data and compute the standard deviation of the remaining 90% of the data points. In this case, the trimming fraction is .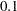

For example, the following statement specifies that the variables Temperature and Catalyst are scaled before performing the loess fitting. In this case, because the trimming fraction is 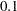, the scale estimate used for each of these variables is a 10% trimmed standard deviation.

 model Yield=Temperature Catalyst / scale = SD(0.1);

The default trimming fraction used by PROC LOESS is 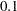and need not be specified by the SCALE= option. Thus the following MODEL statement is equivalent to the previous MODEL statement.

 model Yield=Temperature Catalyst / scale = SD;

If the SCALE= option is not specified, no scaling of the independent variables is done. This is appropriate when there is only a single independent variable or when all the independent variables are a priori scaled similarly.

When the SCALE= option is specified, the scaling details for each independent variable are added to the ScaleDetails table (see Output 50.3.2 for an example). By default, this table contains only the minimum and maximum values of each independent variable in the model. Finally, note that when the SCALE= option is used, specifying the SCALEDINDEP option in the MODEL statement adds the scaled values of the independent variables to the OutputStatistics and PredAtVertices tables. If the SCALEDINDEP option is specified in the SCORE statement, then scaled values of the independent variables are included in the ScoreResults table. By default, only the unscaled values are placed in these tables.