| The LOESS Procedure |
| Local Regression and the Loess Method |
Assume that for  to
to  , the
, the 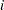 th measurement
th measurement 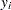 of the response
of the response 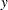 and the corresponding measurement
and the corresponding measurement 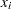 of the vector
of the vector  of
of  predictors are related by
predictors are related by
 |
where  is the regression function and
is the regression function and 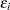 is a random error. The idea of local regression is that at a predictor
is a random error. The idea of local regression is that at a predictor  , the regression function
, the regression function  can be locally approximated by the value of a function in some specified parametric class. Such a local approximation is obtained by fitting a regression surface to the data points within a chosen neighborhood of the point
can be locally approximated by the value of a function in some specified parametric class. Such a local approximation is obtained by fitting a regression surface to the data points within a chosen neighborhood of the point  .
.
In the loess method, weighted least squares is used to fit linear or quadratic functions of the predictors at the centers of neighborhoods. The radius of each neighborhood is chosen so that the neighborhood contains a specified percentage of the data points. The fraction of the data, called the smoothing parameter, in each local neighborhood controls the smoothness of the estimated surface. Data points in a given local neighborhood are weighted by a smooth decreasing function of their distance from the center of the neighborhood.
In a direct implementation, such fitting is done at each point at which the regression surface is to be estimated. A much faster computational procedure is to perform such local fitting at a selected sample of points in predictor space and then to blend these local polynomials to obtain a regression surface.
You can use the LOESS procedure to perform statistical inference provided that the error distribution satisfies some basic assumptions. In particular, such analysis is appropriate when the 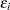 are i.i.d. normal random variables with mean 0. By using the iterative reweighting, the LOESS procedure can also provide statistical inference when the error distribution is symmetric but not necessarily normal. Furthermore, by doing iterative reweighting, you can use the LOESS procedure to perform robust fitting in the presence of outliers in the data.
are i.i.d. normal random variables with mean 0. By using the iterative reweighting, the LOESS procedure can also provide statistical inference when the error distribution is symmetric but not necessarily normal. Furthermore, by doing iterative reweighting, you can use the LOESS procedure to perform robust fitting in the presence of outliers in the data.
While all output of the LOESS procedure can be optionally displayed, most often the LOESS procedure is used to produce output data sets that will be viewed and manipulated by other SAS procedures. PROC LOESS uses the Output Delivery System (ODS) to place results in output data sets. This is a departure from older SAS procedures that provide OUTPUT statements to create SAS data sets from analysis results.
Copyright © SAS Institute, Inc. All Rights Reserved.