Recall from Chapter 3, Introduction to Statistical Modeling with SAS/STAT Software, that the general regression problem is to model the mean of a random vector 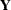as a function of a parameters and covariates in a statistical model. The many forms of regression models have their origin in the characteristics of the response variable (discrete or continuous, normal or nonnormal distributed), assumptions about the form of the model (linear, nonlinear, or generalized linear), assumptions about the data-generating mechanism (survey, observational, or experimental data), and estimation principles. The following procedures, listed in alphabetical order, perform at least one type of regression analysis.

CATMOD

analyzes data that can be represented by a contingency table. PROC CATMOD fits linear models to functions of response frequencies, and it can be used for linear and logistic regression. See Chapter 8, Introduction to Categorical Data Analysis Procedures, and Chapter 28, The CATMOD Procedure, for more information.

GAM

fits generalized additive models. The models fitted with the GAM procedure are nonparameteric in that the usual assumption of a linear predictor is relaxed. The name stems from the fact that the models consist of additive, smooth functions in the regression variables. The GAM procedure can fit additive models to nonnormal data. See Chapter 36, The GAM Procedure, for more information.

GENMOD

fits generalized linear models. PROC GENMOD is especially suited for responses with discrete outcomes, and it performs logistic regression and Poisson regression in addition to fitting generalized estimating equations for repeated measures data. Bayesian analysis capabilities for generalized linear models are also available with the GENMOD procedure. See Chapter 8, Introduction to Categorical Data Analysis Procedures, and Chapter 37, The GENMOD Procedure, for more information.

GLIMMIX

fits generalized linear mixed models by likelihood-based methods. In addition to many other analyses, PROC GLIMMIX can perform simple, multiple, polynomial, and weighted regression. The GLIMMIX procedure can also fit linear mixed models and models without random effects. See Chapter 38, The GLIMMIX Procedure, for more information.

GLM

uses the method of least squares to fit general linear models. In addition to many other analyses, PROC GLM can perform simple, multiple, polynomial, and weighted regression. PROC GLM has many of the same input/output capabilities as PROC REG, but it does not provide as many diagnostic tools or allow interactive changes in the model or data. See Chapter 5, Introduction to Analysis of Variance Procedures, and Chapter 39, The GLM Procedure, for more information.

LIFEREG

fits parametric models to failure-time data that might be right-censored. These types of models are commonly used in survival analysis. See Chapter 14, Introduction to Survey Sampling and Analysis Procedures, and Chapter 48, The LIFEREG Procedure, for more information.

LOESS

fits nonparametric models by using a local regression method. PROC LOESS is suitable for modeling regression surfaces where the underlying parametric form is unknown and where robustness in the presence of outliers is required. See Chapter 50, The LOESS Procedure, for more information.

LOGISTIC

fits logistic models for binomial and ordinal outcomes. PROC LOGISTIC provides a wide variety of model-building methods and computes numerous regression diagnostics. See Chapter 8, Introduction to Categorical Data Analysis Procedures, and Chapter 51, The LOGISTIC Procedure, for more information.

MIXED

fits linear mixed models by likelihood-based techniques. In addition to many other analyses, PROC MIXED can fit models without random effects; hence, the procedure can perform simple, multiple, polynomial, and weighted regression. See Chapter 56, The MIXED Procedure, for more information.

NLIN

fits general nonlinear regression models by the method of nonlinear least squares. Several different iterative methods are available. See Chapter 60, The NLIN Procedure, for more information.

NLMIXED

fits general nonlinear mixed regression models by the method of maximum likelihood. With the NLMIXED procedure you can specify a custom objective function for parameter estimation and fit models with or without random effects. See Chapter 61, The NLMIXED Procedure, for more information.

ORTHOREG

performs regression by using the Gentleman-Givens computational method. For ill-conditioned data, PROC ORTHOREG can produce more accurate parameter estimates than other procedures such as PROC GLM and PROC REG. See Chapter 63, The ORTHOREG Procedure, for more information.

PHREG

fits Cox proportional hazards regression models to survival data. See Chapter 64, The PHREG Procedure, for more information.

PLS

performs partial least squares regression, principal components regression, and reduced rank regression, with cross validation for the number of components. See Chapter 67, The PLS Procedure, for more information.

PROBIT

performs probit regression in addition to logistic regression and ordinal logistic regression. The PROBIT procedure is useful when the dependent variable is either dichotomous or polychotomous and the independent variables are continuous. See Chapter 72, The PROBIT Procedure, for more information.

QUANTREG

models the effects of covariates on the conditional quantiles of a response variable by means of quantile regression. See Chapter 73, The QUANTREG Procedure, for more information.

REG

performs linear regression with many diagnostic capabilities, selects models by using one of nine methods, produces scatter plots of raw data and statistics, highlights scatter plots to identify particular observations, and allows interactive changes in both the regression model and the data that are used to fit the model. See Chapter 74, The REG Procedure, for more information.

ROBUSTREG

performs robust regression by using Huber M estimation and high breakdown value estimation. PROC ROBUSTREG is suitable for detecting outliers and providing resistant (stable) results in the presence of outliers. See Chapter 75, The ROBUSTREG Procedure, for more information.

RSREG

builds quadratic response-surface regression models. PROC RSREG analyzes the fitted response surface to determine the factor levels of optimum response and performs a ridge analysis to search for the region of optimum response. See Chapter 76, The RSREG Procedure, for more information.

SURVEYLOGISTIC

fits logistic models for binary and ordinal outcomes to survey data by maximum likelihood. See Chapter 85, The SURVEYLOGISTIC Procedure, for more information.

SURVEYPHREG

fits proportional hazards models for survey data by maximizing a partial pseudo-likelihood function that incorporates the sampling weights. The procedure provides design-based variance estimates, confidence intervals, and tests for the estimated proportional hazards regression coefficients. See Chapter 87, The SURVEYPHREG Procedure, for more information.

SURVEYREG

fits linear regression models to survey data by generalized least squares by using elementwise regresssion. See Chapter 88, The SURVEYREG Procedure, for more information.

TRANSREG

fits univariate and multivariate linear models, optionally with spline and other nonlinear transformations. Models include ordinary regression and ANOVA, multiple and multivariate regression, metric and nonmetric conjoint analysis, metric and nonmetric vector and ideal point preference mapping, redundancy analysis, canonical correlation, and response surface regression. See Chapter 91, The TRANSREG Procedure, for more information.

Several SAS/ETS procedures also perform regression. The following procedures are documented in the SAS/ETS User’s Guide.

AUTOREG

implements regression models that use time series data where the errors are autocorrelated. See Chapter 8, The AUTOREG Procedure (SAS/ETS 9.22 User's Guide), for more details.

COUNTREG

analyzes regression models in which the dependent variable takes nonnegative integer or count values. See Chapter 10, The COUNTREG Procedure (SAS/ETS 9.22 User's Guide), for more details.

MODEL

handles nonlinear simultaneous systems of equations, such as econometric models. See Chapter 18, The MODEL Procedure (SAS/ETS 9.22 User's Guide), for more details.

PANEL

analyzes a class of linear econometric models that commonly arise when time series and cross-sectional data are combined. See Chapter 19, The PANEL Procedure (SAS/ETS 9.22 User's Guide), for more details.

PDLREG

performs regression analysis with polynomial distributed lags. See Chapter 20, The PDLREG Procedure (SAS/ETS 9.22 User's Guide), for more details.

SYSLIN

handles linear simultaneous systems of equations, such as econometric models. See Chapter 27, The SYSLIN Procedure (SAS/ETS 9.22 User's Guide), for more details.