| Introduction to Statistical Modeling with SAS/STAT Software |
| Important Linear Algebra Concepts |
A matrix  is a rectangular array of numbers. The order of a matrix with
is a rectangular array of numbers. The order of a matrix with  rows and
rows and  columns is
columns is  . The element in row
. The element in row  , column
, column  of
of  is denoted as
is denoted as 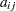 , and the notation
, and the notation  is sometimes used to refer to the two-dimensional row-column array
is sometimes used to refer to the two-dimensional row-column array
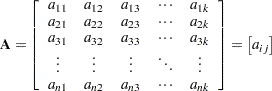 |
A vector is a one-dimensional array of numbers. A column vector has a single column (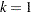 ). A row vector has a single row (
). A row vector has a single row ( ). A scalar is a matrix of order
). A scalar is a matrix of order 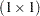 —that is, a single number. A square matrix has the same row and column order,
—that is, a single number. A square matrix has the same row and column order, 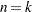 . A diagonal matrix is a square matrix where all off-diagonal elements are zero,
. A diagonal matrix is a square matrix where all off-diagonal elements are zero, 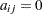 if
if  . The identity matrix
. The identity matrix 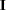 is a diagonal matrix with
is a diagonal matrix with 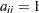 for all
for all  . The unit vector
. The unit vector 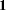 is a vector where all elements are
is a vector where all elements are  . The unit matrix
. The unit matrix 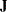 is a matrix of all
is a matrix of all  s. Similarly, the elements of the null vector and the null matrix are all
s. Similarly, the elements of the null vector and the null matrix are all 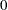 .
.
Basic matrix operations are as follows:
- Addition
If
 and
and 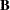 are of the same order, then
are of the same order, then 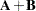 is the matrix of elementwise sums,
is the matrix of elementwise sums, 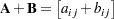
- Subtraction
If
 and
and 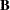 are of the same order, then
are of the same order, then  is the matrix of elementwise differences,
is the matrix of elementwise differences, 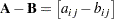
- Dot product
The dot product of two
 -vectors
-vectors  and
and  is the sum of their elementwise products,
is the sum of their elementwise products, 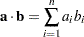
The dot product is also known as the inner product of
 and
and  . Two vectors are said to be orthogonal if their dot product is zero.
. Two vectors are said to be orthogonal if their dot product is zero. - Multiplication
Matrices
 and
and 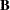 are said to be conformable for
are said to be conformable for 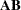 multiplication if the number of columns in
multiplication if the number of columns in  equals the number of rows in
equals the number of rows in  . Suppose that
. Suppose that  is of order
is of order  and that
and that  is of order
is of order  . The product
. The product 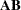 is then defined as the
is then defined as the 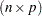 matrix of the dot products of the
matrix of the dot products of the  th row of
th row of  and the
and the  th column of
th column of 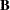 ,
, 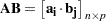
- Transposition
The transpose of the
 matrix
matrix  is denoted as
is denoted as 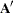 or
or 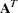 or
or 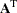 and is obtained by interchanging the rows and columns,
and is obtained by interchanging the rows and columns, 
A symmetric matrix is equal to its transpose,
 . The inner product of two
. The inner product of two 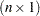 column vectors
column vectors  and
and  is
is  .
.
Matrix Inversion
Regular Inverses
The right inverse of a matrix  is the matrix that yields the identity when
is the matrix that yields the identity when  is postmultiplied by it. Similarly, the left inverse of
is postmultiplied by it. Similarly, the left inverse of  yields the identity if
yields the identity if  is premultiplied by it.
is premultiplied by it.  is said to be invertible and
is said to be invertible and 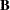 is said to be the inverse of
is said to be the inverse of  , if
, if 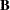 is its right and left inverse,
is its right and left inverse,  . This requires
. This requires  to be square and nonsingular. The inverse of a matrix
to be square and nonsingular. The inverse of a matrix  is commonly denoted as
is commonly denoted as 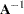 . The following results are useful in manipulating inverse matrices (assuming both
. The following results are useful in manipulating inverse matrices (assuming both  and
and 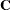 are invertible):
are invertible):
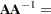 |
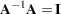 |
|||
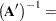 |
 |
|||
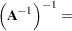 |
 |
|||
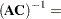 |
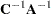 |
|||
 |
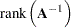 |
If 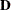 is a diagonal matrix with nonzero entries on the diagonal—that is,
is a diagonal matrix with nonzero entries on the diagonal—that is, 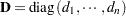 —then
—then 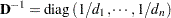 . If
. If 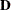 is a block-diagonal matrix whose blocks are invertible, then
is a block-diagonal matrix whose blocks are invertible, then
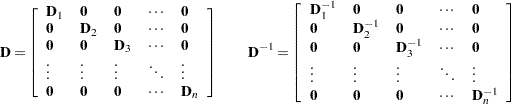 |
In statistical applications the following two results are particularly important, because they can significantly reduce the computational burden in working with inverse matrices.
- Partitioned Matrix
Suppose
 is a nonsingular matrix that is partitioned as
is a nonsingular matrix that is partitioned as 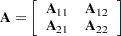
Then, provided that all the inverses exist, the inverse of
 is given by
is given by 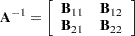
where
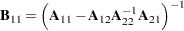 ,
, 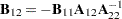 ,
, 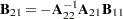 , and
, and 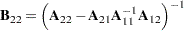 .
. - Patterned Sum
Suppose
 is
is  nonsingular,
nonsingular,  is
is 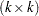 nonsingular, and
nonsingular, and 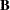 and
and 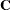 are
are  and
and 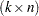 matrices, respectively. Then the inverse of
matrices, respectively. Then the inverse of 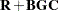 is given by
is given by 
This formula is particularly useful if
 and
and 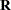 has a simple form that is easy to invert. This case arises, for example, in mixed models where
has a simple form that is easy to invert. This case arises, for example, in mixed models where 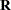 might be a diagonal or block-diagonal matrix, and
might be a diagonal or block-diagonal matrix, and  .
. Another situation where this formula plays a critical role is in the computation of regression diagnostics, such as in determining the effect of removing an observation from the analysis. Suppose that
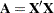 represents the crossproduct matrix in the linear model
represents the crossproduct matrix in the linear model 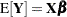 . If
. If 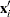 is the
is the  th row of the
th row of the  matrix, then
matrix, then 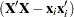 is the crossproduct matrix in the same model with the
is the crossproduct matrix in the same model with the  th observation removed. Identifying
th observation removed. Identifying 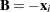 ,
, 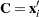 , and
, and 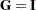 in the preceding inversion formula, you can obtain the expression for the inverse of the crossproduct matrix:
in the preceding inversion formula, you can obtain the expression for the inverse of the crossproduct matrix: 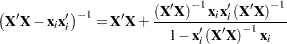
This expression for the inverse of the reduced data crossproduct matrix enables you to compute "leave-one-out" deletion diagnostics in linear models without refitting the model.
Generalized Inverse Matrices
If  is rectangular (not square) or singular, then it is not invertible and the matrix
is rectangular (not square) or singular, then it is not invertible and the matrix 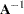 does not exist. Suppose you want to find a solution to simultaneous linear equations of the form
does not exist. Suppose you want to find a solution to simultaneous linear equations of the form
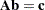 |
If  is square and nonsingular, then the unique solution is
is square and nonsingular, then the unique solution is 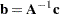 . In statistical applications, the case where
. In statistical applications, the case where  is
is  rectangular is less important than the case where
rectangular is less important than the case where  is a
is a 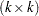 square matrix of rank less than
square matrix of rank less than  . For example, the normal equations in ordinary least squares (OLS) estimation in the model
. For example, the normal equations in ordinary least squares (OLS) estimation in the model  are
are
 |
A generalized inverse matrix is a matrix 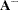 such that
such that  is a solution to the linear system. In the OLS example, a solution can be found as
is a solution to the linear system. In the OLS example, a solution can be found as 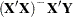 , where
, where 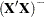 is a generalized inverse of
is a generalized inverse of 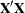 .
.
The following four conditions are often associated with generalized inverses. For the square or rectangular matrix  there exist matrices
there exist matrices 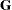 that satisfy
that satisfy
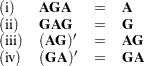 |
The matrix 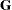 that satisfies all four conditions is unique and is called the Moore-Penrose inverse, after the first published work on generalized inverses by Moore (1920) and the subsequent definition by Penrose (1955). Only the first condition is required, however, to provide a solution to the linear system above.
that satisfies all four conditions is unique and is called the Moore-Penrose inverse, after the first published work on generalized inverses by Moore (1920) and the subsequent definition by Penrose (1955). Only the first condition is required, however, to provide a solution to the linear system above.
Pringle and Rayner (1971) introduced a numbering system to distinguish between different types of generalized inverses. A matrix that satisfies only condition (i) is a  -inverse. The
-inverse. The  -inverse satistifes conditions (i) and (ii). It is also called a reflexive generalized inverse. Matrices satisfying conditions (i)–(iii) or conditions (i), (ii), and (iv) are
-inverse satistifes conditions (i) and (ii). It is also called a reflexive generalized inverse. Matrices satisfying conditions (i)–(iii) or conditions (i), (ii), and (iv) are 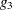 -inverses. Note that a matrix that satisfies the first three conditions is a right generalized inverse, and a matrix that satisfies conditions (i), (ii), and (iv) is a left generalized inverse. For example, if
-inverses. Note that a matrix that satisfies the first three conditions is a right generalized inverse, and a matrix that satisfies conditions (i), (ii), and (iv) is a left generalized inverse. For example, if 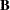 is
is  of rank
of rank  , then
, then 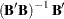 is a left generalized inverse of
is a left generalized inverse of 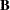 . The notation
. The notation 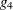 -inverse for the Moore-Penrose inverse, satisfying conditions (i)–(iv), is often used by extension, but note that Pringle and Rayner (1971) do not use it; rather, they call such a matrix "the" generalized inverse.
-inverse for the Moore-Penrose inverse, satisfying conditions (i)–(iv), is often used by extension, but note that Pringle and Rayner (1971) do not use it; rather, they call such a matrix "the" generalized inverse.
If the  matrix
matrix  is rank-deficient—that is,
is rank-deficient—that is, 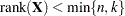 —then the system of equations
—then the system of equations
 |
does not have a unique solution. A particular solution depends on the choice of the generalized inverse. However, some aspects of the statistical inference are invariant to the choice of the generalized inverse. If 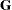 is a generalized inverse of
is a generalized inverse of 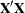 , then
, then 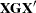 is invariant to the choice of
is invariant to the choice of 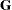 . This result comes into play, for example, when you are computing predictions in an OLS model with a rank-deficient
. This result comes into play, for example, when you are computing predictions in an OLS model with a rank-deficient  matrix, since it implies that the predicted values
matrix, since it implies that the predicted values
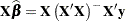 |
are invariant to the choice of 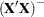 .
.
Matrix Differentiation
Taking the derivative of expressions involving matrices is a frequent task in statistical estimation. Objective functions that are to be minimized or maximized are usually written in terms of model matrices and/or vectors whose elements depend on the unknowns of the estimation problem. Suppose that  and
and 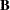 are real matrices whose elements depend on the scalar quantities
are real matrices whose elements depend on the scalar quantities  and
and 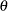 —that is,
—that is, 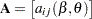 , and similarly for
, and similarly for 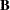 .
.
The following are useful results in finding the derivative of elements of a matrix and of functions involving a matrix. For more in-depth discussion of matrix differentiation and matrix calculus, see, for example, Magnus and Neudecker (1999) and Harville (1997).
The derivative of  with respect to
with respect to  is denoted
is denoted 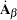 and is the matrix of the first derivatives of the elements of
and is the matrix of the first derivatives of the elements of  :
:
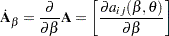 |
Similarly, the second derivative of  with respect to
with respect to  and
and 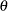 is the matrix of the second derivatives
is the matrix of the second derivatives
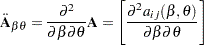 |
The following are some basic results involving sums, products, and traces of matrices:
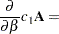 |
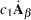 |
|||
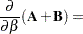 |
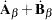 |
|||
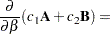 |
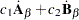 |
|||
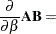 |
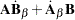 |
|||
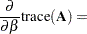 |
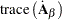 |
|||
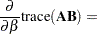 |
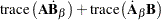 |
The next set of results is useful in finding the derivative of elements of  and of functions of
and of functions of  , if
, if  is a nonsingular matrix:
is a nonsingular matrix:
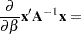 |
 |
|||
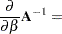 |
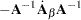 |
|||
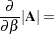 |
 |
|||
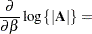 |
 |
|||
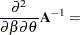 |
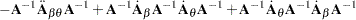 |
|||
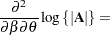 |
 |
Now suppose that  and
and  are column vectors that depend on
are column vectors that depend on  and/or
and/or 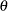 and that
and that  is a vector of constants. The following results are useful for manipulating derivatives of linear and quadratic forms:
is a vector of constants. The following results are useful for manipulating derivatives of linear and quadratic forms:
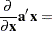 |
 |
|||
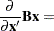 |
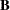 |
|||
 |
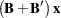 |
|||
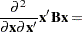 |
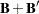 |
Matrix Decompositions
To decompose a matrix is to express it as a function—typically a product—of other matrices that have particular properties such as orthogonality, diagonality, triangularity. For example, the Cholesky decomposition of a symmetric positive definite matrix  is
is 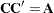 , where
, where 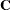 is a lower-triangular matrix. The spectral decomposition of a symmetric matrix is
is a lower-triangular matrix. The spectral decomposition of a symmetric matrix is  , where
, where 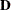 is a diagonal matrix and
is a diagonal matrix and  is an orthogonal matrix.
is an orthogonal matrix.
Matrix decomposition play an important role in statistical theory as well as in statistical computations. Calculations in terms of decompositions can have greater numerical stability. Decompositions are often necessary to extract information about matrices, such as matrix rank, eigenvalues, or eigenvectors. Decompositions are also used to form special transformations of matrices, such as to form a "square-root" matrix. This section briefly mentions several decompositions that are particularly prevalent and important.
LDU, LU, and Cholesky Decomposition
Every square matrix  , whether it is positive definite or not, can be expressed in the form
, whether it is positive definite or not, can be expressed in the form  , where
, where 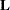 is a unit lower-triangular matrix,
is a unit lower-triangular matrix, 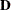 is a diagonal matrix, and
is a diagonal matrix, and 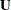 is a unit upper-triangular matrix. (The diagonal elements of a unit triangular matrix are 1.) Because of the arrangement of the matrices, the decomposition is called the LDU decomposition. Since you can absorb the diagonal matrix into the triangular matrices, the decomposition
is a unit upper-triangular matrix. (The diagonal elements of a unit triangular matrix are 1.) Because of the arrangement of the matrices, the decomposition is called the LDU decomposition. Since you can absorb the diagonal matrix into the triangular matrices, the decomposition
 |
is also referred to as the LU decomposition of  .
.
If the matrix  is positive definite, then the diagonal elements of
is positive definite, then the diagonal elements of 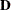 are positive and the LDU decomposition is unique. Furthermore, we can add more specificity to this result in that for a symmetric, positive definite matrix, there is a unique decomposition
are positive and the LDU decomposition is unique. Furthermore, we can add more specificity to this result in that for a symmetric, positive definite matrix, there is a unique decomposition  , where
, where 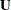 is unit upper-triangular and
is unit upper-triangular and 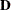 is diagonal with positive elements. Absorbing the square root of
is diagonal with positive elements. Absorbing the square root of 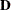 into
into 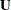 ,
, 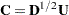 , the decomposition is known as the Cholesky decomposition of a positive-definite matrix:
, the decomposition is known as the Cholesky decomposition of a positive-definite matrix:
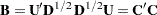 |
where 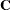 is upper triangular.
is upper triangular.
If 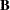 is
is 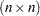 symmetric nonnegative definite of rank
symmetric nonnegative definite of rank  , then we can extend the Cholesky decomposition as follows. Let
, then we can extend the Cholesky decomposition as follows. Let  denote the lower-triangular matrix such that
denote the lower-triangular matrix such that
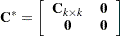 |
Then 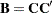 .
.
Spectral Decomposition
Suppose that  is an
is an 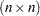 symmetric matrix. Then there exists an orthogonal matrix
symmetric matrix. Then there exists an orthogonal matrix 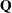 and a diagonal matrix
and a diagonal matrix 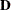 such that
such that 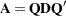 . Of particular importance is the case where the orthogonal matrix is also orthonormal—that is, its column vectors have unit norm. Denote this orthonormal matrix as
. Of particular importance is the case where the orthogonal matrix is also orthonormal—that is, its column vectors have unit norm. Denote this orthonormal matrix as  . Then the corresponding diagonal matrix—
. Then the corresponding diagonal matrix—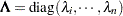 , say—contains the eigenvalues of
, say—contains the eigenvalues of  . The spectral decomposition of
. The spectral decomposition of  can be written as
can be written as
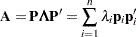 |
where 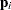 denotes the
denotes the  th column vector of
th column vector of  . The right-side expression decomposes
. The right-side expression decomposes  into a sum of rank-1 matrices, and the weight of each contribution is equal to the eigenvalue associated with the
into a sum of rank-1 matrices, and the weight of each contribution is equal to the eigenvalue associated with the  th eigenvector. The sum furthermore emphasizes that the rank of
th eigenvector. The sum furthermore emphasizes that the rank of  is equal to the number of nonzero eigenvalues.
is equal to the number of nonzero eigenvalues.
Harville (1997, p. 538) refers to the spectral decomposition of  as the decomposition that takes the previous sum one step further and accumulates contributions associated with the distinct eigenvalues. If
as the decomposition that takes the previous sum one step further and accumulates contributions associated with the distinct eigenvalues. If 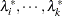 are the distinct eigenvalues and
are the distinct eigenvalues and 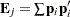 , where the sum is taken over the set of columns for which
, where the sum is taken over the set of columns for which 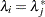 , then
, then
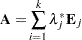 |
You can employ the spectral decomposition of a nonnegative definite symmetric matrix to form a "square-root" matrix of  . Suppose that
. Suppose that  is the diagonal matrix containing the square roots of the
is the diagonal matrix containing the square roots of the  . Then
. Then 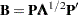 is a square-root matrix of
is a square-root matrix of  in the sense that
in the sense that  , because
, because
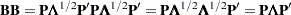 |
Generating the Moore-Penrose inverse of a matrix based on the spectral decomposition is also simple. Denote as 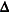 the diagonal matrix with typical element
the diagonal matrix with typical element
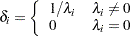 |
Then the matrix 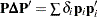 is the Moore-Penrose (
is the Moore-Penrose (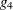 -generalized) inverse of
-generalized) inverse of  .
.
Singular-Value Decomposition
The singular-value decomposition is related to the spectral decomposition of a matrix, but it is more general. The singular-value decomposition can be applied to any matrix. Let 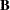 be an
be an 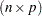 matrix of rank
matrix of rank  . Then there exist orthogonal matrices
. Then there exist orthogonal matrices 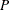 and
and  of order
of order 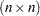 and
and  , respectively, and a diagonal matrix
, respectively, and a diagonal matrix 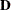 such that
such that
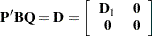 |
where 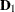 is a diagonal matrix of order
is a diagonal matrix of order  . The diagonal elements of
. The diagonal elements of 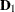 are strictly positive. As with the spectral decomposition, this result can be written as a decomposition of
are strictly positive. As with the spectral decomposition, this result can be written as a decomposition of 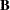 into a weighted sum of rank-1 matrices
into a weighted sum of rank-1 matrices
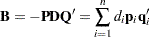 |
The scalars 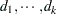 are called the singular values of the matrix
are called the singular values of the matrix 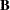 . They are the positive square roots of the nonzero eigenvalues of the matrix
. They are the positive square roots of the nonzero eigenvalues of the matrix 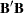 . If the singular-value decomposition is applied to a symmetric, nonnegative definite matrix
. If the singular-value decomposition is applied to a symmetric, nonnegative definite matrix  , then the singular values
, then the singular values  are the nonzero eigenvalues of
are the nonzero eigenvalues of  and the singular-value decomposition is the same as the spectral decomposition.
and the singular-value decomposition is the same as the spectral decomposition.
As with the spectral decomposition, you can use the results of the singular-value decomposition to generate the Moore-Penrose inverse of a matrix. If 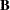 is
is 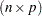 with singular-value decomposition
with singular-value decomposition 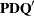 , and if
, and if 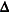 is a diagonal matrix with typical element
is a diagonal matrix with typical element
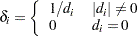 |
then 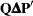 is the
is the 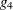 -generalized inverse of
-generalized inverse of 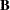 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.