Overview: Categorical Data Analysis Procedures

There are two approaches to performing categorical data analyses. The first computes statistics based on tables defined by categorical variables (variables that assume only a limited number of discrete values), performs hypothesis tests about the association between these variables, and requires the assumption of a randomized process; following Stokes, Davis, and Koch (2000), call these methods randomization procedures. The other approach investigates the association by modeling a categorical response variable, regardless of whether the explanatory variables are continuous or categorical; call these methods modeling procedures. Several procedures in SAS/STAT software can be used for the analysis of categorical data.

The randomization procedures are:

FREQ

builds frequency tables or contingency tables and can produce numerous statistics. For one-way frequency tables, it can perform tests for equal proportions, specified proportions, or the binomial proportion. For contingency tables, it can compute various tests and measures of association and agreement including chi-square statistics, odds ratios, correlation statistics, Fisher’s exact test for any size two-way table, kappa, and trend tests. In addition, it performs stratified analysis, computing Cochran-Mantel-Haenszel statistics and estimates of the common relative risk. Exact 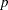-values and confidence intervals are available for various test statistics and measures. See Chapter 35, The FREQ Procedure, for more information.

SURVEYFREQ

incorporates complex sample designs to analyze one-way, two-way, and multiway crosstabulation tables. Estimates population totals and proportions and performs tests of goodness-of-fit and independence. See Chapter 14, Introduction to Survey Sampling and Analysis Procedures, and Chapter 84, The SURVEYFREQ Procedure, for more information.

The modeling procedures, which require a categorical response variable, are:

CATMOD

fits linear models to functions of categorical data, facilitating such analyses as regression, analysis of variance, linear modeling, log-linear modeling, logistic regression, and repeated measures analysis. Maximum likelihood estimation is used for the analysis of logits and generalized logits, and weighted least squares analysis is used for fitting models to other response functions. Iterative proportional fitting (IPF), which avoids the need for parameter estimation, is available for fitting hierarchical log-linear models when there is a single population. See Chapter 28, The CATMOD Procedure, for more information.

GENMOD

fits generalized linear models with maximum-likelihood methods. This family includes logistic, probit, and complementary log-log regression models for binomial data, Poisson and negative binomial regression models for count data, and multinomial models for ordinal response data. It performs likelihood ratio and Wald tests for Type I, Type III, and user-defined contrasts. It analyzes repeated measures data with generalized estimating equation (GEE) methods. Bayesian analysis capabilities for generalized linear models are also available. See Chapter 37, The GENMOD Procedure, for more information.

GLIMMIX

fits generalized linear mixed models with maximum-likelihood methods. If the model does not contain random effects, the GLIMMIX procedure fits generalized linear models by the method of maximum likelihood. This family includes logistic, probit, and complementary log-log regression models for binomial data, Poisson and negative binomial regression models for count data, and multinomial models for ordinal response data. See Chapter 38, The GLIMMIX Procedure, for more information.

LOGISTIC

fits linear logistic regression models for discrete response data with maximum-likelihood methods. It provides four variable selection methods, computes regression diagnostics, and compares and outputs receiver operating characteristic curves. It can also perform stratified conditional logistic regression analysis for binary response data and exact conditional regression analysis for binary and nominal response data. The logit link function in the logistic regression models can be replaced by the probit function or the complementary log-log function. See Chapter 51, The LOGISTIC Procedure, for more information.

PROBIT

fits models with probit, logit, or complementary log-log links for quantal assay or other discrete event data. It is mainly designed for dose-response analysis with a natural response rate. It computes the fiducial limits for the dose variable and provides various graphical displays for the analysis. See Chapter 72, The PROBIT Procedure, for more information.

SURVEYLOGISTIC

fits logistic models for binary and ordinal outcomes to survey data by maximum likelihood, incorporating complex survey sample designs. See Chapter 85, The SURVEYLOGISTIC Procedure, for more information.

Also see Chapter 3, Introduction to Statistical Modeling with SAS/STAT Software, and Chapter 4, Introduction to Regression Procedures, for more information about all the modeling and regression procedures.

Other procedures that can be used for categorical data analysis and modeling are:

CORRESP

performs simple and multiple correspondence analyses, using a contingency table, Burt table, binary table, or raw categorical data as input. See Chapter 9, Introduction to Multivariate Procedures, and Chapter 30, The CORRESP Procedure, for more information.

PRINQUAL

performs a principal component analysis of qualitative and/or quantitative data, and multidimensional preference analysis. See Chapter 9, Introduction to Multivariate Procedures, and Chapter 71, The PRINQUAL Procedure, for more information.

TRANSREG

fits univariate and multivariate linear models, optionally with spline and other nonlinear transformations. Models include ordinary regression and ANOVA, multiple and multivariate regression, metric and nonmetric conjoint analysis, metric and nonmetric vector and ideal point preference mapping, redundancy analysis, canonical correlation, and response surface regression. See Chapter 4, Introduction to Regression Procedures, and Chapter 91, The TRANSREG Procedure, for more information.