A Type 1 analysis consists of fitting a sequence of models, beginning with a simple model with only an intercept term, and continuing through a model of specified complexity, fitting one additional effect on each step. Likelihood ratio statistics—that is, twice the difference of the log likelihoods—are computed between successive models. This type of analysis is sometimes called an analysis of deviance since, if the dispersion parameter is held fixed for all models, it is equivalent to computing differences of scaled deviances. The asymptotic distribution of the likelihood ratio statistics, under the hypothesis that the additional parameters included in the model are equal to 0, is a chi-square with degrees of freedom equal to the difference in the number of parameters estimated in the successive models. Thus, these statistics can be used in a test of hypothesis of the significance of each additional term fit.

This type of analysis is not available for GEE models, since the deviance is not computed for this type of model.

If the dispersion parameter 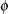is known, it can be included in the models; if it is unknown, there are two strategies allowed by PROC GENMOD. The dispersion parameter can be estimated from a maximal model by the deviance or Pearson’s chi-square divided by degrees of freedom, as discussed in the section Goodness of Fit, and this value can be used in all models. An alternative is to consider the dispersion to be an additional unknown parameter for each model and estimate it by maximum likelihood on each step. By default, PROC GENMOD estimates scale by maximum likelihood at each step.

A table of likelihood ratio statistics is produced, along with associated 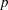-values based on the asymptotic chi-square distributions.

If you specify either the SCALE=DEVIANCE or the SCALE=PEARSON option in the MODEL statement, the dispersion parameter is estimated using the deviance or Pearson’s chi-square statistic, and 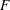statistics are computed in addition to the chi-square statistics for assessing the significance of each additional term in the Type 1 analysis. See the section F Statistics for a definition of 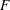statistics.

This Type 1 analysis has the general property that the results depend on the order in which the terms of the model are fitted. The terms are fitted in the order in which they are specified in the MODEL statement.