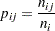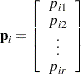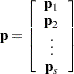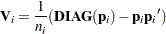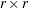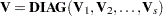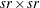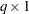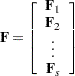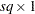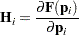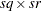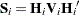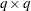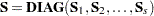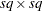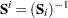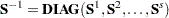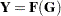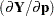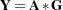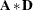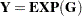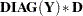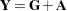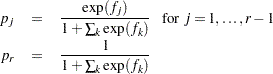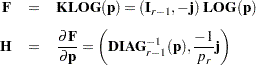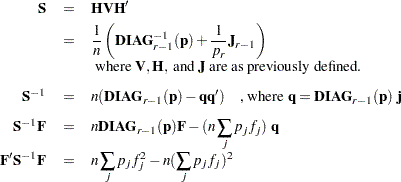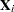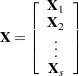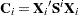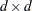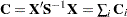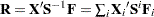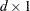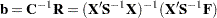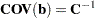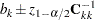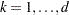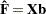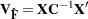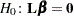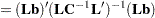| The CATMOD Procedure |
| Computational Formulas |
The following formulas are shown for each population and for all populations combined.
Source |
Formula |
Dimension |
|
|---|---|---|---|
Probability Estimates |
|||
|
|
|
|
|
|
|
|
all populations |
|
|
|
Variance of Probability Estimates |
|||
|
|
|
|
all populations |
|
|
|
Response Functions |
|||
|
|
|
|
all populations |
|
|
|
Derivative of Function with Respect to Probability Estimates |
|||
|
|
|
|
all populations |
|
|
|
Variance of Functions |
|||
|
|
|
|
all populations |
|
|
|
Inverse Variance of Functions |
|||
|
|
|
|
all populations |
|
|
|
Derivative Table for Compound Functions: Y=F(G(p))
In the following table, let 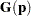 be a vector of functions of
be a vector of functions of 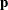 , and let
, and let 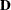 denote
denote 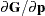 , which is the first derivative matrix of
, which is the first derivative matrix of 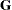 with respect to
with respect to 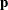 :
:
Function |
|
Derivative |
|---|---|---|
Multiply matrix |
|
|
Logarithm |
|
|
Exponential |
|
|
Add constant |
|
|
Default Response Functions: Generalized Logits
In the following table, subscripts 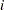 for the population are suppressed. Also denote
for the population are suppressed. Also denote 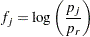 for
for 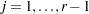 for each population
for each population  .
.
Formula |
|
|---|---|
Inverse of Response Functions for a Population |
|
|
|
Form of F and Derivative for a Population |
|
|
|
Covariance Results for a Population |
|
|
|
The following calculations are shown for each population and then for all populations combined:
Source |
Formula |
Dimension |
|
|---|---|---|---|
Design Matrix |
|||
|
|
|
|
all populations |
|
|
|
Crossproduct of Design Matrix |
|||
|
|
|
|
all populations |
|
|
|
In the following table, 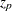 is the 100
is the 100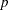 th percentile of the standard normal distribution:
th percentile of the standard normal distribution:
Formula |
Dimension |
|
|---|---|---|
Crossproduct of Design Matrix with Function |
||
|
|
|
Weighted Least Squares Estimates |
||
|
|
|
Covariance of Weighted Least Squares Estimates |
||
|
|
|
Wald Confidence Limits for Parameter Estimates |
||
|
|
|
Predicted Response Functions |
||
|
|
|
Covariance of Predicted Response Functions |
||
|
|
|
Residual Chi-Square |
||
RSS |
|
|
Chi-Square for |
||
Q |
|
|
Maximum Likelihood Method
Let 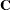 be the Hessian matrix and
be the Hessian matrix and 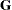 be the gradient of the log-likelihood function (both functions of
be the gradient of the log-likelihood function (both functions of 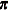 and the parameters
and the parameters  ). Let
). Let 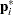 denote the vector containing the first
denote the vector containing the first 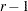 sample proportions from population
sample proportions from population 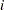 , and let
, and let 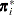 denote the corresponding vector of probability estimates from the current iteration. Starting with the least squares estimates
denote the corresponding vector of probability estimates from the current iteration. Starting with the least squares estimates 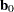 of
of  (if you use the ML and WLS options; with the ML option alone, the procedure starts with
(if you use the ML and WLS options; with the ML option alone, the procedure starts with 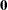 ), the probabilities
), the probabilities 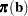 are computed, and
are computed, and  is calculated iteratively by the Newton-Raphson method until it converges (see the EPSILON= option). The factor
is calculated iteratively by the Newton-Raphson method until it converges (see the EPSILON= option). The factor 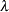 is a step-halving factor that equals one at the start of each iteration. For any iteration in which the likelihood decreases, PROC CATMOD uses a series of subiterations in which
is a step-halving factor that equals one at the start of each iteration. For any iteration in which the likelihood decreases, PROC CATMOD uses a series of subiterations in which 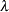 is iteratively divided by two. The subiterations continue until the likelihood is greater than that of the previous iteration. If the likelihood has not reached that point after 10 subiterations, then convergence is assumed, and a warning message is displayed.
is iteratively divided by two. The subiterations continue until the likelihood is greater than that of the previous iteration. If the likelihood has not reached that point after 10 subiterations, then convergence is assumed, and a warning message is displayed.
Sometimes, infinite parameters are present in the model, either because of the presence of one or more zero frequencies or because of a poorly specified model with collinearity among the estimates. If an estimate is tending toward infinity, then PROC CATMOD flags the parameter as infinite and holds the estimate fixed in subsequent iterations. PROC CATMOD regards a parameter to be infinite when two conditions apply:
The absolute value of its estimate exceeds five divided by the range of the corresponding variable.
The standard error of its estimate is at least three times greater than the estimate itself.
The estimator of the asymptotic covariance matrix of the maximum likelihood predicted probabilities is given by Imrey, Koch, and Stokes (1981, eq. 2.18).
The following equations summarize the method:
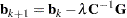 |
where
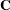 |
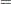 |
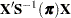 |
|||
 |
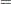 |
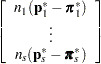 |
|||
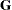 |
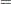 |
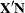 |
Iterative Proportional Fitting
The algorithm used by PROC CATMOD for iterative proportional fitting is described in Bishop, Fienberg, and Holland (1975), Haberman (1972), and Agresti (2002). To illustrate the method, consider the observed three-dimensional table 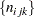 for the variables X, Y, and Z, and the following hierarchical model:
for the variables X, Y, and Z, and the following hierarchical model:
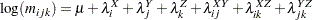 |
The following statements request that PROC CATMOD use IPF to fit the preceding model:
model X*Y*Z = _response_ / ml=ipf; loglin X|Y|Z@2;
Begin with a table of initial cell estimates 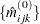 . PROC CATMOD produces the initial estimates by setting the
. PROC CATMOD produces the initial estimates by setting the 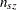 structural zero cells to 0 and all other cells to
structural zero cells to 0 and all other cells to 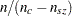 , where
, where  is the total weight of the table and
is the total weight of the table and  is the total number of cells in the table. Iteratively adjust the estimates at step
is the total number of cells in the table. Iteratively adjust the estimates at step  to the observed marginal tables specified in the model by cycling through the following three-stage process to produce the estimates at step
to the observed marginal tables specified in the model by cycling through the following three-stage process to produce the estimates at step  :
:
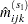 |
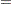 |
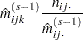 |
|||
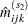 |
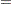 |
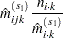 |
|||
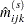 |
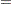 |
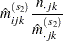 |
The subscript " " indicates summation over the missing subscript. The log-likelihood
" indicates summation over the missing subscript. The log-likelihood 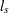 is estimated at each step
is estimated at each step  by
by
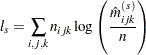 |
When the function 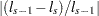 is less than
is less than 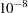 , the iterations terminate. You can change the comparison value with the EPSILON= option, and you can change the convergence criterion with the CONVCRIT= option. The option CONVCRIT=CELL uses the maximum cell difference
, the iterations terminate. You can change the comparison value with the EPSILON= option, and you can change the convergence criterion with the CONVCRIT= option. The option CONVCRIT=CELL uses the maximum cell difference
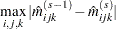 |
as the criterion while the option CONVCRIT=MARGIN computes the maximum difference of the margins
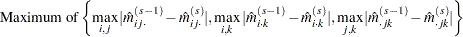 |
Copyright © SAS Institute, Inc. All Rights Reserved.
 th response
th response