| The TTEST Procedure |
Interpreting Graphs
Agreement Plots for Paired Designs
For paired designs, the second response of each pair is plotted against the first response, with the mean shown as a large bold symbol. If the WEIGHT statement is used, then the mean is the weighted mean. A diagonal line with slope=0 and y-intercept=1 is overlaid. The location of the points with respect to the diagonal line reveals the strength and direction of the difference or ratio. The tighter the clustering along the same direction as the line, the stronger the positive correlation of the two measurements for each subject. Clustering along a direction perpendicular to the line indicates negative correlation.
Period Agreement Plots for Crossover Designs
The response in the second period is plotted against the response in the first period, with plot symbols distinguishing the two treatment sequences and the two sequence means shown larger in bold. If the WEIGHT statement is used, then the means are weighted means. A diagonal line with slope=0 and y-intercept=1 is overlaid.
In the absence of a strong period effect, the points from each sequence will appear as mirror images about the diagonal line, farther apart with stronger treatment effects. Deviations from symmetry about the diagonal line indicate a period effect. The spread of points within each treatment sequence is an indicator of between-subject variability. The tighter the clustering along the same direction as the line (within each treatment sequence), the stronger the positive correlation of the two measurements for each subject. Clustering along a direction perpendicular to the line indicates negative correlation.
The period agreement plot is usually less informative than the treatment agreement plot. The exception is when the period effect is stronger than the treatment effect.
Treatment Agreement Plots for Crossover Designs
The response associated with the second treatment is plotted against the response associated with the first treatment, with plot symbols distinguishing the two treatment sequences and the two sequence means shown larger in bold. If the WEIGHT statement is used, then the means are weighted means. A diagonal line with slope=0 and y-intercept=1 is overlaid.
The location of the points with respect to the diagonal line reveals the strength and direction of the treatment effect. Substantial location differences between the two sequences indicates a strong period effect. The spread of points within each treatment sequence is an indicator of between-subject variability. The tighter the clustering along the same direction as the line (within each treatment sequence), the stronger the positive correlation of the two measurements for each subject. Clustering along a direction perpendicular to the line indicates negative correlation.
Box Plots
The box is drawn from the  th percentile (lower quartile) to the
th percentile (lower quartile) to the 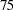 th percentile (upper quartile). The vertical line inside the box shows the location of the median. If DIST=NORMAL, then a diamond symbol shows the location of the mean. The whiskers extend to the minimum and maximum observations, and circles beyond the whiskers identify outliers.
th percentile (upper quartile). The vertical line inside the box shows the location of the median. If DIST=NORMAL, then a diamond symbol shows the location of the mean. The whiskers extend to the minimum and maximum observations, and circles beyond the whiskers identify outliers.
For one-sample and paired designs, a confidence interval for the mean is shown as a band in the background. If the analysis is an equivalence analysis (with the TOST option in the PROC TTEST statement), then the interval is a 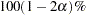 confidence interval shown along with the equivalence bounds. The inclusion of this interval completely within the bounds is indicative of a significant
confidence interval shown along with the equivalence bounds. The inclusion of this interval completely within the bounds is indicative of a significant  -value. If the analysis is not an equivalence analysis, then the confidence level is
-value. If the analysis is not an equivalence analysis, then the confidence level is 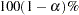 . If the SHOWH0 global plot option is used, then the null value for the test is shown. If the WEIGHT statement is used, then weights are incorporated in the confidence intervals.
. If the SHOWH0 global plot option is used, then the null value for the test is shown. If the WEIGHT statement is used, then weights are incorporated in the confidence intervals.
Histograms
The WEIGHT statement is ignored in the computation of the normal and kernel densities.
Confidence Intervals
If the analysis is an equivalence analysis (with the TOST option in the PROC TTEST statement), then unless the TYPE=PERGROUP option is used, the interval is a 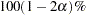 mean confidence interval shown along with the equivalence bounds. The inclusion of this interval completely within the bounds is indicative of a significant
mean confidence interval shown along with the equivalence bounds. The inclusion of this interval completely within the bounds is indicative of a significant  -value.
-value.
If the analysis is not an equivalence analysis, or if the TYPE=PERGROUP option is used, then the confidence level is 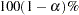 . If the SHOWH0 global plot option is used, then the null value for the test is shown.
. If the SHOWH0 global plot option is used, then the null value for the test is shown.
If the SIDES=L or SIDES=U option is used in the PROC TTEST statement, then the unbounded side of the one-sided interval is represented with an arrowhead. Note that the actual location of the arrowhead is irrelevant.
If the WEIGHT statement is used, then weights are incorporated in the confidence intervals.
Profiles for Paired Designs
For paired designs, a line is drawn for each observation from left to right connecting the first response to the second response. The mean first response and mean second response are connected with a bold line. If the WEIGHT statement is used, then the means are weighted means. The more extreme the slope, the stronger the effect. A wide spread of profiles indicates high between-subject variability. Consistent positive slopes indicate strong positive correlation. Widely varying slopes indicate lack of correlation, while consistent negative slopes indicate strong negative correlation.
Profiles over Period for Crossover Designs
For each observation, the response for the first period is connected to the response for second period, regardless of the treatment applied in each period. The means for each treatment sequence are shown in bold. If the WEIGHT statement is used, then the means are weighted means.
In the absence of a strong period effect, the profiles for each sequence will appear as mirror images about an imaginary horizontal line in the center. Deviations from symmetry about this imaginary horizontal line indicate a period effect. A wide spread of profiles within sequence indicates high between-subject variability.
The TYPE=PERIOD plot is usually less informative than the TYPE=TREATMENT plot. The exception is when the period effect is stronger than the treatment effect.
Profiles over Treatment for Crossover Designs
For each observation, the response for the first treatment is connected to the response for the second treatment, regardless of the periods in which they occur. The means for each treatment sequence are shown in bold. If the WEIGHT statement is used, then the means are weighted means.
In general, the more extreme the slope, the stronger the treatment effect. Slope differences between the two treatment sequences measure the period effect. A wide spread of profiles within sequence indicates high between-subject variability.
Q-Q Plots
Q-Q plots are useful for diagnosing violations of the normality and homoscedasticity assumptions. If the data in a Q-Q plot come from a normal distribution, the points will cluster tightly around the reference line. You can use the UNIVARIATE procedure with the NORMAL option to numerically check the normality assumption.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.