 |
|
| The TPSPLINE Procedure |
| Computational Formulas |
The theoretical foundations for the thin-plate smoothing spline are described in Duchon (1976, 1977) and Meinguet (1979). Further results and applications are given in Wahba and Wendelberger (1980), Hutchinson and Bischof (1983), and Seaman and Hutchinson (1985).
Suppose that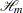 
is a space of functions whose partial derivatives of total order 
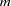are in 
, where 
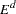is the domain of 
.
Now, consider the data model
 |
where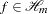 
.
Using the notation from the section Penalized Least Squares Estimation, for a fixed 
, estimate 
by minimizing the penalized least squares function
 |
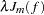is the penalty term to enforce smoothness on . There are several ways to define 
. For the thin-plate smoothing spline, with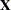 
of dimension 
, define as
 |
where 
. Under this definition, will give zero penalty to some functions. The space that is spanned by the set of polynomials contributing zero penalty is called the polynomial space. The dimension of the polynomial space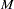 
is a function of dimension and order 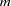of the smoothing penalty.
When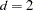 
and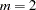 
, is as follows:
 |
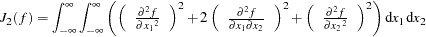and 
.
In general, 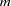and must satisfy the condition that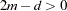 
. For the sake of simplicity, the formulas and equations that follow assume 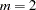. See Wahba (1990) and Bates et al. (1987) for more details.
Duchon (1976) showed that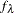 
can be represented as
 |
where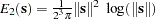 
for 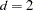. For derivations of 
for other values of , see Villalobos and Wahba (1987).
If you define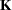 
with elements 
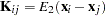and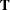 
with elements 
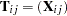, the goal is to find coefficients 
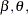and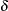 
that minimize
 |
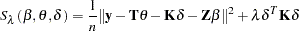A unique solution is guaranteed if the matrix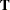 
is of full rank and 
.
If 
and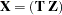 
, the expression for 
becomes
 |
The coefficients 
and 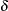can be obtained by solving
 |
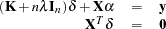To compute and 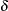, let the QR decomposition of 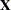be
 |
where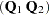 
is an orthogonal matrix and 
is an upper triangular, with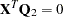 
(Dongarra et al. 1979).
Since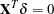 
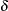, must be in the column space of 
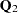. Therefore, 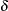can be expressed as 
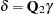for a vector 
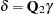. Substituting into the preceding equation and multiplying through by 
gives
 |
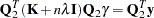or
 |
The coefficient can be obtained by solving
 |
The influence matrix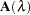 
is defined as
 |
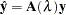and has the form
 |
Similar to the regression case, and if you consider the trace of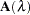 
as the degrees of freedom for the model and the trace of 
as the degrees of freedom for the error, the estimate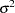 
can be represented as
 |
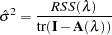where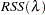 
is the residual sum of squares. Theoretical properties of these estimates have not yet been published. However, good numerical results in simulation studies have been described by several authors. For more information, see O’Sullivan and Wong (1987), Nychka (1986a, 1986b, 1988), and Hall and Titterington (1987).
Confidence Intervals
Viewing the spline model as a Bayesian model, Wahba (1983) proposed Bayesian confidence intervals for smoothing spline estimates as follows:
 |
where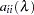 
is the 
th diagonal element of the 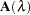matrix and 
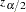is the 
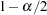quantile of the standard normal distribution. The confidence intervals are interpreted as intervals "across the function" as opposed to pointwise intervals.
Suppose that you fit a spline estimate that consists of a true function and a random error term, 
, to experimental data. In repeated experiments, it is likely that about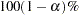 
of the confidence intervals cover the corresponding true values, although some values are covered every time and other values are not covered by the confidence intervals most of the time. This effect is more pronounced when the true surface or surface has small regions of particularly rapid change.
Smoothing Parameter
The quantity is called the smoothing parameter, which controls the balance between the goodness of fit and the smoothness of the final estimate.
A large heavily penalizes the 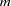th derivative of the function, thus forcing 
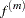close to 0. A small places less of a penalty on rapid change in 
, resulting in an estimate that tends to interpolate the data points.
The smoothing parameter greatly affects the analysis, and it should be selected with care. One method is to perform several analyses with different values for and compare the resulting final estimates.
A more objective way to select the smoothing parameter is to use the "leave-out-one" cross validation function, which is an approximation of the predicted mean squares error. A generalized version of the leave-out-one cross validation function is proposed by Wahba (1990) and is easy to calculate. This generalized cross validation (GCV) function is defined as
 |
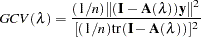The justification for using the GCV function to select relies on asymptotic theory. Thus, you cannot expect good results for very small sample sizes or when there is not enough information in the data to separate the model from the error component. Simulation studies suggest that for independent and identically distributed Gaussian noise, you can obtain reliable estimates of for 
greater than 
or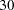 
. Note that, even for large values of (say,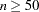 
), in extreme Monte Carlo simulations there might be a small percentage of unwarranted extreme estimates in which 
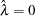or 
(Wahba 1983). Generally, if 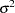is known to within an order of magnitude, the occasional extreme case can be readily identified. As gets larger, the effect becomes weaker.
The GCV function is fairly robust against nonhomogeneity of variances and non-Gaussian errors (Villalobos and Wahba 1987). Andrews (1988) has provided favorable theoretical results when variances are unequal. However, this selection method is likely to give unsatisfactory results when the errors are highly correlated.
The GCV value might be suspect when is extremely small because computed values might become indistinguishable from zero. In practice, calculations with 
or near 0 can cause numerical instabilities resulting in an unsatisfactory solution. Simulation studies have shown that a with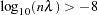 
is small enough that the final estimate based on this almost interpolates the data points. A GCV value based on a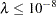 
might not be accurate.
|
|
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.