| The TPSPLINE Procedure |
| MODEL Statement |
- MODEL dependents = <regression variables> (smoothing variables) </options> ;
The MODEL statement specifies the dependent variables, the independent regression variables, which are listed with no parentheses, and the independent smoothing variables, which are listed inside parentheses.
The regression variables are optional. At least one smoothing variable is required, and it must be listed after the regression variables. No variables can be listed in both the regression variable list and the smoothing variable list.
If you specify more than one dependent variable, PROC TPSPLINE calculates a thin-plate smoothing spline estimate for each dependent variable, by using the regression variables and smoothing variables specified on the right side.
If you specify regression variables, PROC TPSPLINE fits a semiparametric model by using the regression variables as the linear part of the model.
You can specify the following options in the MODEL statement.
- ALPHA=number
specifies the significance level
 of the confidence limits on the final thin-plate smoothing spline estimate when you request confidence limits to be included in the output data set. Specify number as a value between 0 and 1. The default value is
of the confidence limits on the final thin-plate smoothing spline estimate when you request confidence limits to be included in the output data set. Specify number as a value between 0 and 1. The default value is 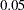 . See the section OUTPUT Statement for more information about the OUTPUT statement.
. See the section OUTPUT Statement for more information about the OUTPUT statement. - DF=number
specifies the degrees of freedom of the thin-plate smoothing spline estimate, defined as
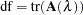
where
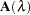 is the hat matrix. Specify number as a value between zero and the number of unique design points
is the hat matrix. Specify number as a value between zero and the number of unique design points 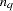 . Smaller
. Smaller 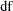 values cause more penalty on the roughness and thus smoother fits.
values cause more penalty on the roughness and thus smoother fits. - DISTANCE=number
- D=number
defines a range such that if the
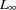 distance between two data points
distance between two data points 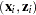 and
and 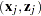 satisfies
satisfies 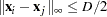
then these data points are treated as replicates, where
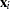 are the smoothing variables and
are the smoothing variables and 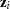 are the regression variables.
are the regression variables. You can use the DISTANCE= option to reduce the number of unique design points by treating nearby data as replicates. This can be useful when you have a large data set. Larger DISTANCE= option values cause fewer
 points. The default value is 0.
points. The default value is 0. PROC TPSPLINE uses the DISTANCE= value to group points as follows: The data are first sorted by the smoothing variables in the order in which they appear in the MODEL statement. The first point in the sorted data becomes the first unique point. Subsequent points have their x-values set equal to that point until the first point where the maximum distance in one dimension is larger than
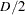 . This point becomes the next unique point, and so on. Because of this sequential processing, the set of unique points differs depending on the order of the smoothing variables in the MODEL statement.
. This point becomes the next unique point, and so on. Because of this sequential processing, the set of unique points differs depending on the order of the smoothing variables in the MODEL statement. For example, with a model that has two smoothing variables (x1,x2), the data are first sorted by x1 and x2 (in that order), and then uniqueness is assessed sequentially. The first point in the sorted data
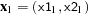 becomes the first unique point,
becomes the first unique point, 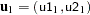 . Subsequent points
. Subsequent points  are set equal to
are set equal to 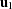 until the algorithm comes to a point with
until the algorithm comes to a point with 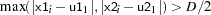 . This point becomes the second unique point
. This point becomes the second unique point 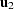 , and we proceed from there.
, and we proceed from there. - LAMBDA0=number
specifies the smoothing parameter,
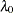 , to be used in the thin-plate smoothing spline estimate. By default, PROC TPSPLINE uses the
, to be used in the thin-plate smoothing spline estimate. By default, PROC TPSPLINE uses the  parameter that minimizes the GCV function for the final fit. The LAMBDA0= value must be positive. Larger
parameter that minimizes the GCV function for the final fit. The LAMBDA0= value must be positive. Larger 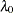 values cause smoother fits.
values cause smoother fits. - LAMBDA=list-of-values
specifies a set of values for the
 parameter. PROC TPSPLINE returns a GCV value for each
parameter. PROC TPSPLINE returns a GCV value for each  point that you specify. You can use the LAMBDA= option to study the GCV function curve for a set of values for
point that you specify. You can use the LAMBDA= option to study the GCV function curve for a set of values for  . All values listed in the LAMBDA= option must be positive.
. All values listed in the LAMBDA= option must be positive. - LOGNLAMBDA0=number
- LOGNL0=number
specifies the smoothing parameter
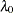 on the
on the 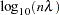 scale. If you specify both the LOGNL0= and LAMBDA0= options, only the value provided by the LOGNL0= option is used. Larger
scale. If you specify both the LOGNL0= and LAMBDA0= options, only the value provided by the LOGNL0= option is used. Larger  values cause smoother fits. By default, PROC TPSPLINE uses the
values cause smoother fits. By default, PROC TPSPLINE uses the  parameter that minimizes the GCV function for the estimate.
parameter that minimizes the GCV function for the estimate. - LOGNLAMBDA=list-of-values
- LOGNL=list-of-values
specifies a set of values for the
 parameter on the
parameter on the 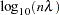 scale. PROC TPSPLINE returns a GCV value for each
scale. PROC TPSPLINE returns a GCV value for each  point that you specify. You can use the LOGNLAMBDA= option to study the GCV function curve for a set of
point that you specify. You can use the LOGNLAMBDA= option to study the GCV function curve for a set of  values. If you specify both the LOGNL= and LAMBDA= options, only the list of values provided by the LOGNL= option is used.
values. If you specify both the LOGNL= and LAMBDA= options, only the list of values provided by the LOGNL= option is used. In some cases, the LOGNL= option might be preferred over the LAMBDA= option. Because the LAMBDA= value must be positive, a small change in that value can result in a major change in the GCV value. If you instead specify
 on the
on the 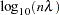 scale, the allowable range is enlarged to include negative values. Thus, the GCV function is less sensitive to changes in LOGNLAMBDA.
scale, the allowable range is enlarged to include negative values. Thus, the GCV function is less sensitive to changes in LOGNLAMBDA. The DF= option, LAMBDA0= option, and LOGNLAMBDA0= option all specify exact smoothness of a nonparametric fit. If you want to fit a model with specified smoothness, the DF= option is preferable to the other two options because
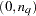 , the range of
, the range of 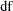 , is much smaller in length than
, is much smaller in length than 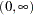 of
of  and
and 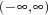 of
of 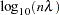 .
. - M=number
specifies the order of the derivative in the penalty term. The M= value must be a positive integer. The default value is
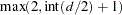 , where
, where  is the number of smoothing variables.
is the number of smoothing variables.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.