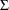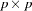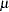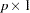PROC TCALIS: The MSTRUCT Model :: SAS/STAT(R) 9.2 User's Guide, Second Edition

The TCALIS Procedure

The MSTRUCT Model

In contrast to other modeling languages where the mean and covariance structures are implied from the specification of equations, paths, variable-factor relations, mean parameters, variance parameters, or covariance parameters, the MSTRUCT modeling language is supported in PROC TCALIS for modeling mean and covariance structures directly.

A simple example for using the MSTRUCT modeling language is the testing of a covariance model with equal variances and covariances. Suppose that a variable was measured five times in an experiment. The covariance matrix of these five measurements is hypothesized to have the following structure:

$\text{[math]}$

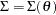where

$\text{[math]}$

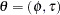and

$\text{[math]}$

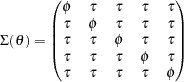For model structures that are hypothesized directly on the covariance matrix, the MSTRUCT modeling language is the most convenient to use. You can also use other general modeling languages such as LINEQS, PATH, or RAM to fit the same model structures, but the specification is less straightforward and more error-prone. For convenience, models specified using the MSTRUCT modeling language are called MSTRUCT models.

Model Matrices in the MSTRUCT Model

Suppose that there are $\text{[math]}$ observed variables. The two model matrices, their names, their roles, and their dimensions are summarized in the following table:

Matrix	Name	Description	Dimensions
$\text{[math]}$	_COV_ or _MSTRUCTCOV_	structured covariance matrix	$\text{[math]}$
$\text{[math]}$	_MEAN_ or _MSTRUCTMEAN_	structured mean vector	$\text{[math]}$

Specification of the MSTRUCT Model

Specifying Variables

In the MSTRUCT statement, you specify the list of $\text{[math]}$ manifest variables of interest in the VAR= list. For example, you specify v1–v5 as the variables analyzed in your MSTRUCT model by this statement:

   mstruct VAR= v1 v2 v3 v4 v5;

See the MSTRUCT statement for details about the syntax.

The manifest variables in the VAR= list must be referenced in the input set. The number of variables in the VAR= list determines the dimensions of the _COV_ and the _MEAN_ matrices in the model. In addition, the order of variables determines the order of row and column variables in the model matrices.

Specifying Parameters in Model Matrices

Denote the parameter vector in the MSTRUCT model as 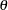$\text{[math]}$ . The dimension of 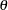$\text{[math]}$ depends on your hypothesized model. In the preceding example, 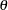$\text{[math]}$ contains two parameters in 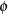$\text{[math]}$ and $\text{[math]}$ . You can use the MATRIX statement to specify these parameters in the _COV_ matrix:

   matrix _COV_ [1,1] = 5*phi,  /* phi for all diagonal elements */
                [2, ] = tau,    /* tau for all off-diagonal elements */
                [3, ] = 2*tau,    
                [4, ] = 3*tau,    
                [5, ] = 4*tau;

In this MATRIX statement, the five diagonal elements, starting from the [1,1] element of the covariance matrix, are fitted by the phi parameter. The specification 5*phi is a short-hand for specifying phi five times, respectively for each of the five diagonal elements in the covariance matrix. All other lower triangular elements are fitted by the tau parameter, as shown in the MATRIX statement. For example, with [3,] the elements starting from the first element of the third row of the _COV_ matrix are parameterized by the tau parameter. The specification 2*tau repeats the specification two times, meaning that the [3,1] and [3,2] elements are both fitted by the same parameter tau. Similarly, all lower triangular elements (not including the diagonal elements) of the _COV_ matrix are fitted by the tau parameter. The specification of the upper triangular elements (diagonal excluded) of the _COV_ matrix is not needed because the _COV_ matrix is symmetric. The specification in the lower triangular elements is transferred automatically to the upper triangular elements. See the MATRIX statement for details about the syntax.

Default Parameters in the MSTRUCT Model

You can specify either fixed values or parameters (with or without initial values) for the elements in the _COV_ and _MEAN_ model matrices. If some elements are not specified, default parameters are applied. There are two types of default parameters: one is automatic free parameters, and the other is fixed zeros. They are applied in different situations.

Automatic Free Parameters

If no MATRIX statements are used to specify parameters in your model matrices, automatic free parameters are generated for all elements in the _COV_ matrix. For example, if you do not use the MATRIX statement to specify any element in the _COV_ matrix, free parameters are generated for all variances and covariances in the _COV_ matrix in the model. Similarly, free parameters are generated for the _MEAN_ vector when the mean structures are invoked by the MEANSTR option in the PROC TCALIS or MODEL statement. Each automatic free parameter is named with a prefix _Add and appended with a unique integer.

Default Fixed Zeros

If you specify at least one parameter (fixed or free) for an element in a model matrix using the MATRIX statement, no automatic free parameters will be generated for that matrix. All unspecified locations in the _COV_ and _MEAN_ model matrices are fixed zeros by default.

How and Why the Default Parameters Are Treated Differently in the MSTRUCT Model

Notice that the default parameter treatment in the MSTRUCT model is different from other types of models. For example, in the LINEQS model variances of and covariances among exogenous manifest variables are all automatic free parameters. These automatic free parameters are generated by PROC TCALIS. In the MSTRUCT model, however, automatic free parameters are either generated for all elements in a model matrix (when nothing is specified for the matrix or when the MATRIX statement is not used for the MSTRUCT model) or not generated at all (when at least one element in the _COV_ matrix is specified).

The reason is that there is no distinction between exogenous (independent) and endogenous (dependent) variables in the MSTRUCT model. Automatic free parameters for variances of, and covariances among, exogenous manifest variables are thus irrelevant.

Because of the particular default parameter treatment, when fitting an MSTRUCT model you must make sure that each diagonal element in your _COV_ matrix is set as a free, constrained, or fixed parameter, in accordance with your theoretical model. If you specify some elements in the model matrix but omit the specification of some diagonal elements, the default zero variances would lead to a nonpositive definite _COV_ model matrix, making the model fitting problematic.

Note: This procedure is experimental.

Top of Page