Theoretical Development

It is a simple matter to produce an 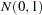random number, and by stacking 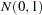random numbers in a column vector, you can obtain a vector with independent standard normal components 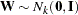. The meaning of the terms independence and randomness in the context of a deterministic algorithm required for the generation of these numbers is subtle; refer to Knuth (1981, Chapter 3) for details.

Rather than 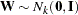, what is required is the generation of a vector 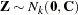—that is,

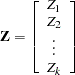with covariance matrix

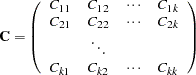If the covariance matrix is symmetric and positive definite, it has a Cholesky root such that 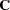can be factored as

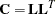where is lower triangular. Refer to Ralston and Rabinowitz (1978, Chapter 9, Section 3-3) for details. This vector 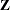can be generated by the transformation 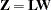. Note that this is where the assumption of a Gaussian SRF is crucial. When 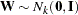, then 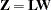is also Gaussian. The mean of 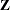is

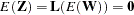and the variance is

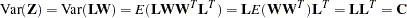Consider now an SRF 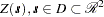, with spatial covariance function 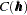. Fix locations 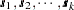, and let 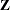denote the random vector

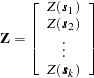with corresponding covariance matrix

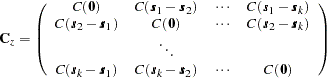Since this covariance matrix is symmetric and positive definite, it has a Cholesky root, and the 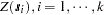, can be simulated as described previously. This is how the SIM2D procedure implements unconditional simulation in the zero-mean case. More generally,

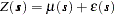with 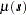being a quadratic form in the coordinates 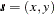, and the 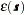being an SRF having the same covariance matrix 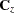as previously. In this case, the 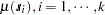, is computed once and added to the simulated vector 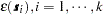, for each realization.

For a conditional simulation, this distribution of

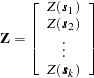must be conditioned on the observed data. The relevant general result concerning conditional distributions of multivariate normal random variables is the following. Let 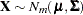, where

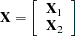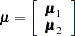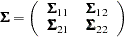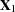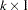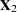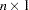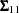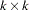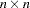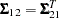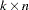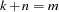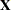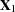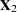The subvector is , is , is , is , and is , with . The full vector is partitioned into two subvectors, and , and 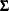is similarly partitioned into covariances and cross covariances.

With this notation, the distribution of 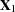conditioned on 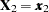is 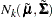, with

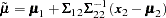and

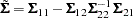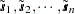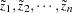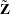Refer to Searle (1971, pp. 46–47) for details. The correspondence with the conditional spatial simulation problem is as follows. Let the coordinates of the observed data points be denoted , with values . Let denote the random vector

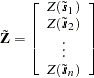The random vector 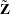corresponds to 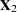, while 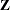corresponds to 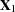. Then 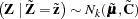as in the previous distribution. The matrix

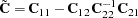is again positive definite, so a Cholesky factorization can be performed.

The dimension for 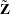is simply the number of nonmissing observations for the VAR= variable; the values 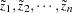are the values of this variable. The coordinates 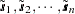are also found in the DATA= data set, with the variables corresponding to the and coordinates identified in the COORDINATES statement. Note that all VAR= variables use the same set of conditioning coordinates; this fixes the matrix 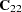for all simulations.

The dimension for 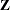is the number of grid points specified in the GRID statement. Since there is a single GRID statement, this fixes the matrix 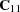for all simulations. Similarly, 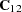is fixed.

The Cholesky factorization 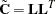is computed once, as is the mean correction

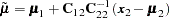Note that the means 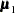and 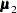are computed using the grid coordinates 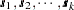, the data coordinates 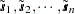, and the quadratic form specification from the MEAN statement. The simulation is now performed exactly as in the unconditional case. A 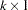vector of independent standard 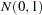random variables is generated and multiplied by , and is added to the transformed vector. This is repeated 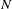times, where 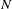is the value specified for the NR= option.