In a group sequential clinical trial, the information level for the observed test statistic generally does not match the corresponding information level in the BOUNDARY= data set. In this situation, the SEQTEST procedure first modifies the information levels at future interim stages to accommodate the information level for the test statistic and computes the error spending values at the current and future stages. The SEQTEST procedure then derives boundary values at the current and future stages for the trial with these new error spending values.

Denote the information level at stage 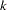for the -stage design stored in the BOUNDARY= data set by 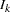, 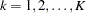. Also denote the information level that corresponds to the test statistic at an interim stage 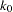by 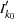, 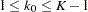. Then for the updated design, the information level at stage 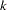, , 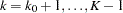is computed as

Note that if 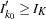, the information level at stage 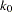reaches the maximum information level in the design, the trial stops at stage 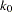, and no future information levels are derived.

The BOUNDARYADJ= option provides various methods to compute error spending values for these new information levels at the current and future interim stages.

The BOUNDARYADJ=NONE option keeps the error spending the same at each stage. The BOUNDARYADJ=ERRLINE option uses a linear interpolation on the cumulative error spending in the design stored in the BOUNDARY= data set to derive the error spending for each unmatched information level (Kittelson and Emerson 1999, p. 882). That is, the cumulative error spending for an information level is computed as

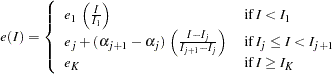where 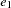, , 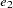..., 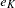are the cumulative errors at the stages of the design that is stored in the BOUNDARY= data set.

The BOUNDARYADJ=ERRFUNCPOC option uses Pocock-type cumulative error spending function (Lan and DeMets 1983):

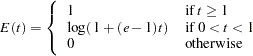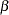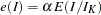With an error level of or , the cumulative error spending for an information level is or .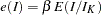

The BOUNDARYADJ=ERRFUNCOBF option uses O’Brien-Fleming-type cumulative error spending function (Lan and DeMets 1983):

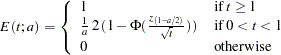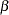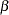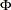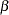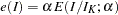where is either for the spending function or for the spending function, and is the cumulative distribution function of the standardized statistic. That is, with an error level of or , the cumulative error spending for an information level is or .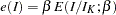

The BOUNDARYADJ=ERRFUNCGAMMA option uses gamma cumulative error spending function (Hwang, Shih, and DeCani 1990):

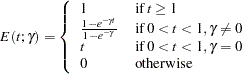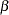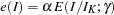where is the parameter specified in the GAMMA= option. That is, with an error level of or , the cumulative error spending for an information level is or .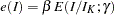

The BOUNDARYADJ=ERRFUNCPOW option uses power cumulative error spending function (Jennison and Turnbull 2000, p. 148):

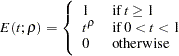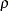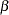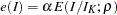where is the power parameter specified in the RHO= suboption. With an error level of or , the cumulative error spending for an information level is or .

If the BOUNDARYKEY=BOTH option is specified, the maximum information (information level at the final stage) required for the trial might not be the same as the maximum information level stored in the BOUNDARY= data set. In this case, the information levels at future stages are adjusted proportionally, and the same error spending values that were computed based on the maximum information level stored in the BOUNDARY= data set are used to derive boundary values for the trial.

If an error spending function is used to create boundaries for the original design in the SEQDESIGN procedure, then in order to better maintain the design features throughout the group sequential trial, the same error spending function to create boundaries for the original design in the SEQDESIGN procedure should be used to modify boundaries in the SEQTEST procedure at each subsequent stage.