Rank Tests for Two Survival Curves (TEST=LOGRANK, TEST=GEHAN, TEST=TARONEWARE)

The method is from Lakatos (1988) and Cantor (1997, pp. 83–92).

Define the following notation:

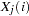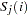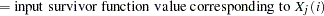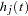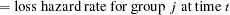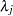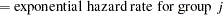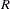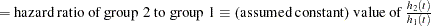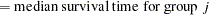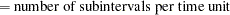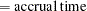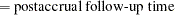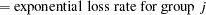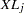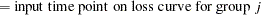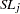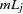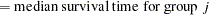Each survival curve can be specified in one of several ways.

• For exponential curves:

  • a single point 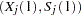on the curve

  • median survival time

  • hazard rate

  • hazard ratio (for curve 2, with respect to curve 1)

• For piecewise linear curves with proportional hazards:

  • a set of points 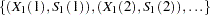(for curve 1)

  • hazard ratio (for curve 2, with respect to curve 1)

• For arbitrary piecewise linear curves:

  • a set of points

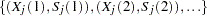
A total of 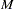evenly spaced time points 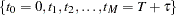are used in calculations, where

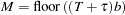The hazard function is calculated for each survival curve at each time point. For an exponential curve, the (constant) hazard is given by one of the following, depending on the input parameterization:

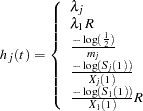For a piecewise linear curve, define the following additional notation:

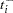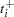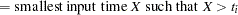The hazard is computed by using linear interpolation as follows:

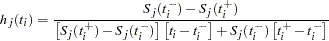With proportional hazards, the hazard rate of group 2’s curve in terms of the hazard rate of group 1’s curve is

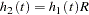Hazard function values for the loss curves are computed in an analogous way from .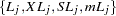

The expected number at risk 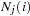at time in group 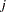is calculated for each group and time points 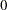through 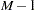, as follows:

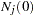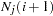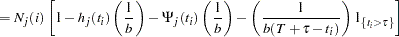Define 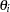as the ratio of hazards and 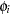as the ratio of expected numbers at risk for time :

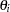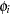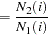The expected number of deaths in each subinterval is calculated as follows:

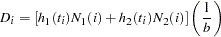The rank values are calculated as follows according to which test statistic is used:

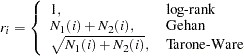The distribution of the test statistic is approximated by where

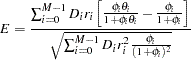Note that can be factored out of the mean 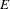, and so it can be expressed equivalently as

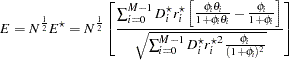where 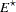is free of 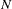and

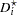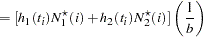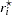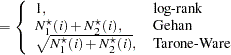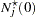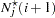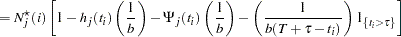The approximate power is

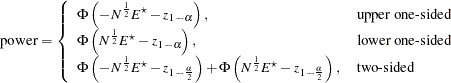Note that the upper and lower one-sided cases are expressed differently than in other analyses. This is because 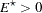corresponds to a higher survival curve in group 1 and thus, by the convention used in PROC power for two-group analyses, the lower side.

For the one-sided cases, a closed-form inversion of the power equation yield an approximate total sample size

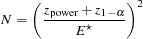For the two-sided case, the solution for 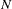is obtained by numerically inverting the power equation.