| The PHREG Procedure |
| CLASS Variable Parameterization |
Consider a model with one CLASS variable A with four levels, 1, 2, 5, and 7. Details of the possible choices for the PARAM= option follow.
- EFFECT
Three columns are created to indicate group membership of the nonreference levels. For the reference level, all three dummy variables have a value of
 . For instance, if the reference level is 7 (REF=7), the design matrix columns for A are as follows:
. For instance, if the reference level is 7 (REF=7), the design matrix columns for A are as follows: Design Matrix
A
A1
A2
A5




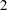







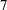



Parameter estimates of CLASS main effects, using the effect coding scheme, estimate the difference in the effect of each nonreference level compared to the average effect over all four levels.
- GLM
As in PROC GLM, four columns are created to indicate group membership. The design matrix columns for A are as follows:
Design Matrix
A
A1
A2
A5
A7





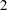









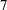




Parameter estimates of CLASS main effects, using the GLM coding scheme, estimate the difference in the effects of each level compared to the last level.
- ORDINAL
Three columns are created to indicate group membership of the higher levels of the effect. For the first level of the effect (which for A is 1), all three dummy variables have a value of 0. The design matrix columns for A are as follows:
Design Matrix
A
A2
A5
A7




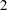







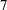



In the ORDINAL coding scheme, the first level of the effect is a control or baseline level. Parameter estimates of CLASS main effects estimate the differences between effects of successive levels. When the parameters have the same sign, the effect is monotonic across the levels.
- POLYNOMIAL
- POLY
Three columns are created. The first represents the linear term (
 ), the second represents the quadratic term (
), the second represents the quadratic term (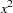 ), and the third represents the cubic term (
), and the third represents the cubic term ( ), where
), where  is the level value. If the CLASS levels are not numeric, they are translated into 1, 2, 3,
is the level value. If the CLASS levels are not numeric, they are translated into 1, 2, 3,  according to their sorting order. The design matrix columns for A are as follows:
according to their sorting order. The design matrix columns for A are as follows: Design Matrix
A
APOLY1
APOLY2
APOLY3




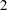
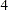
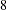




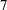
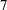
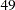
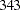
- REFERENCE
- REF
Three columns are created to indicate group membership of the nonreference levels. For the reference level, all three dummy variables have a value of 0. For instance, if the reference level is 7 (REF=7), the design matrix columns for A are as follows:
Design Matrix
A
A1
A2
A5




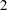







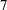



Parameter estimates of CLASS main effects, using the reference coding scheme, estimate the difference in the effect of each nonreference level compared to the effect of the reference level.
- ORTHEFFECT
The columns are obtained by applying the Gram-Schmidt orthogonalization to the columns for PARAM=EFFECT. The design matrix columns for A are as follows:
Design Matrix
A
AOEFF1
AOEFF2
AOEFF3

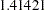

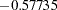
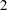
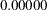
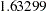
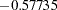

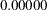
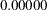

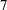
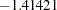
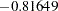
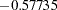
- ORTHORDINAL
The columns are obtained by applying the Gram-Schmidt orthogonalization to the columns for PARAM=ORDINAL. The design matrix columns for A are as follows:
Design Matrix
A
AOORD1
AOORD2
AOORD3


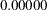
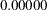
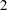
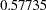
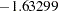
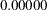

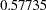

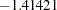
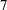
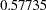

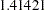
- ORTHPOLY
The columns are obtained by applying the Gram-Schmidt orthogonalization to the columns for PARAM=POLY. The design matrix columns for A are as follows:
Design Matrix
A
AOPOLY1
AOPOLY2
AOPOLY5

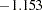
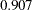
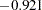
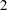

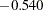
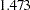

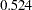
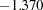
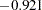
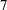

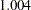
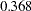
- ORTHREF
The columns are obtained by applying the Gram-Schmidt orthogonalization to the columns for PARAM=REFERENCE. The design matrix columns for A are as follows:
Design Matrix
A
AOREF1
AOREF2
AOREF3


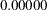
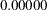
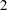
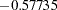
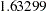
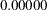

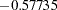

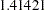
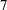
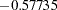

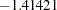
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.