| The PHREG Procedure |
Posterior Distribution for Quantities of Interest
Let 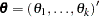 be the parameter vector. For the Cox model, the
be the parameter vector. For the Cox model, the 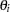 ’s are the regression coefficients
’s are the regression coefficients 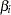 ’s, and for the piecewise constant baseline hazard model, the
’s, and for the piecewise constant baseline hazard model, the 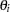 ’s consist of the baseline hazards
’s consist of the baseline hazards 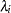 ’s (or log baseline hazards
’s (or log baseline hazards 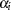 ’s) and the regression coefficients
’s) and the regression coefficients 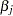 ’s. Let
’s. Let 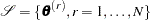 be the chain representing the posterior distribution for
be the chain representing the posterior distribution for  .
.
Consider a quantity of interest  that can be expressed as a function
that can be expressed as a function 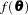 of the parameter vector
of the parameter vector  . You can construct the posterior distribution of
. You can construct the posterior distribution of  by evaluating the function
by evaluating the function 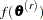 for each
for each 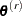 in
in  . The posterior chain for
. The posterior chain for  is
is 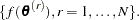 Summary statistics such as mean, standard deviation, percentiles, and credible intervals are used to describe the posterior distribution of
Summary statistics such as mean, standard deviation, percentiles, and credible intervals are used to describe the posterior distribution of  .
.
Hazard Ratio
As shown in the section Hazard Ratios, a log-hazard ratio is a linear combination of the regression coefficients. Let 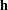 be the vector of linear coefficients. The posterior sample for this hazard ratio is the set
be the vector of linear coefficients. The posterior sample for this hazard ratio is the set  .
.
Survival Distribution
Let  be a covariate vector of interest.
be a covariate vector of interest.
Cox Model
Let  be the observed data. Define
be the observed data. Define
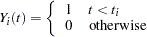 |
Consider the  th draw
th draw  of
of  . The baseline cumulative hazard function at time
. The baseline cumulative hazard function at time  is given by
is given by
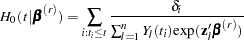 |
For the given covariate vector  , the cumulative hazard function at time
, the cumulative hazard function at time  is
is
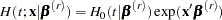 |
and the survival function at time  is
is
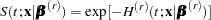 |
Piecewise Exponential Model
Let  be a partition of the time axis. Consider the
be a partition of the time axis. Consider the  th draw
th draw 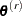 in
in  , where
, where 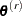 consists of
consists of  and
and  . The baseline cumulative hazard function at time
. The baseline cumulative hazard function at time  is
is
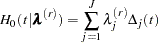 |
where
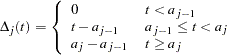 |
For the given covariate vector  , the cumulative hazard function at time
, the cumulative hazard function at time  is
is
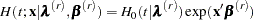 |
and the survival function at time  is
is
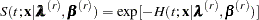 |
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.