| The PHREG Procedure |
Sampling from the Posterior Distribution
PROC PHREG uses a Gibbs sampler to generate the posterior samples. See the section Gibbs Sampler for a general discussion.
Let 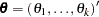 be the parameter vector. For the Cox model, the
be the parameter vector. For the Cox model, the 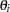 ’s are the regression coefficients
’s are the regression coefficients 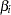 ’s, and for the piecewise constant baseline hazard model, the
’s, and for the piecewise constant baseline hazard model, the 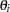 ’s consist of the baseline hazards
’s consist of the baseline hazards 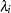 ’s (or log baseline hazards
’s (or log baseline hazards 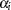 ’s) and the regression coefficients
’s) and the regression coefficients 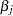 ’s. Let
’s. Let  be the likelihood function, where
be the likelihood function, where  is the observed data. Note that for the Cox model, the likelihood contains the infinite-dimensional baseline hazard function and the Gamma process is perhaps the most commonly used prior process (Ibrahim, Chen, and Sinha; 2001); however, Sinha, Ibrahim, and Chen (2003) justify using the partial likelihood as the likelihood function for the Bayesian analysis. Let
is the observed data. Note that for the Cox model, the likelihood contains the infinite-dimensional baseline hazard function and the Gamma process is perhaps the most commonly used prior process (Ibrahim, Chen, and Sinha; 2001); however, Sinha, Ibrahim, and Chen (2003) justify using the partial likelihood as the likelihood function for the Bayesian analysis. Let 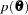 be the prior distribution. The full conditional distribution of
be the prior distribution. The full conditional distribution of 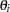 is proportional to the joint distribution; that is,
is proportional to the joint distribution; that is,
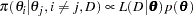 |
For instance, the one-dimensional conditional distribution of 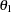 given
given 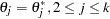 , is computed as
, is computed as
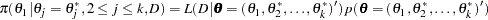 |
Suppose you have a set of arbitrary starting values 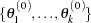 . Using the ARMS (adaptive rejection Metropolis sampling) algorithm of Gilks, Best, and Tan (1995), you do the following:
. Using the ARMS (adaptive rejection Metropolis sampling) algorithm of Gilks, Best, and Tan (1995), you do the following:
draw
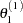 from
from 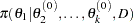
draw
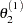 from
from 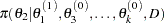

draw
 from
from 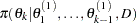
This completes one iteration of the Gibbs sampler. After one iteration, you have 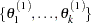 . After
. After  iterations, you have
iterations, you have 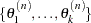 .
.
You can output these posterior samples into a SAS data set through ODS. The following SAS statement outputs the posterior samples into the SAS data set Post:
ods output PosteriorSample=Post;
The data set also includes the variable LogPost, representing the log of the posterior log likelihood.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.