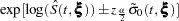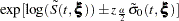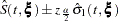Product-Limit Estimates

Let 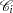denote the set of individuals censored in the half-open interval 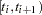, where 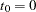and . Let denote the censoring times in 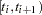; l ranges over .

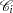The likelihood function for all individuals is given by

where is empty. The likelihood 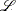is maximized by taking 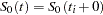for 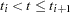and allowing the probability mass to fall only on the observed event times 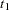, , 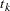. By considering a discrete model with hazard contribution at , you take 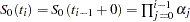, where . Substitution into the likelihood function produces

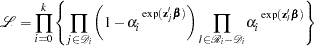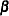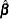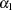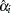If you replace with estimated from the partial likelihood function and then maximize with respect to , , , the maximum likelihood estimate of 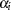becomes a solution of

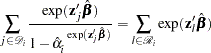When only a single failure occurs at 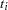, 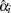can be found explicitly. Otherwise, an iterative solution is obtained by the Newton method.

The estimated baseline cumulative hazard function is

where is the estimated baseline survivor function given by

For details, refer to Kalbfleisch and Prentice (1980). For a given realization of the explanatory variables , the product-limit estimate of the survival function at 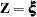is

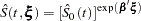Empirical Cumulative Hazards Function Estimates

Let be a given realization of the explanatory variables. The empirical cumulative hazard function estimate at 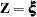is

The variance estimator of is given by the following (Tsiatis; 1981):

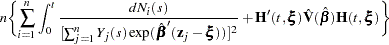where 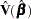is the estimated covariance matrix of 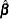and

For the marginal model, the variance estimator computation follows Spiekerman and Lin (1998).

The empirical cumulative hazard function (CH) estimate of the survivor function for 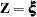is

Confidence Intervals for the Survivor Function

Let 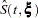and 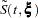correspond to the product-limit (PL) and empirical cumulative hazard function (CH) estimates of the survivor function for 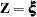, respectively. Both the standard error of log(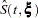) and the standard error of log(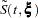) are approximated by 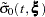, which is the square root of the variance estimate of ; refer to Kalbfleisch and Prentice (1980, p. 116). By the delta method, the standard errors of 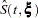and 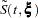are given by

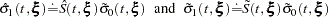respectively. The standard errors of log[–log(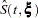)] and log[–log(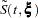)] are given by

respectively.

Let 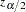be the upper 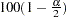percentile point of the standard normal distribution. A 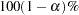confidence interval for the survivor function 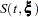is given in the following table.