| The PHREG Procedure |
Confidence Limits for a Hazard Ratio
Let 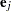 be the
be the 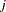 th unit vector—that is, the
th unit vector—that is, the 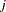 th entry of the vector is 1 and all other entries are 0. The hazards ratio for the explanatory variable with regression coefficient
th entry of the vector is 1 and all other entries are 0. The hazards ratio for the explanatory variable with regression coefficient 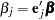 is defined as
is defined as 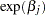 . In general, a log-hazard ratio can be written as
. In general, a log-hazard ratio can be written as 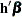 , a linear combination of the regression coefficients, and the hazard ratio
, a linear combination of the regression coefficients, and the hazard ratio 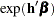 is obtained by replacing
is obtained by replacing 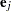 with
with 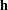 .
.
Point Estimate
The hazards ratio 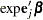 is estimated by
is estimated by 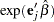 , where
, where 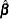 is the maximum likelihood estimate of the
is the maximum likelihood estimate of the 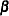 .
.
Wald’s Confidence Limits
The 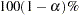 confidence limits for the hazard ratio are calculated as
confidence limits for the hazard ratio are calculated as
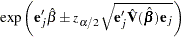 |
where 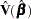 is estimated covariance matrix, and
is estimated covariance matrix, and 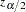 is the
is the 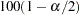 percentile point of the standard normal distribution.
percentile point of the standard normal distribution.
Profile-Likelihood Confidence Limits
The construction of the profile-likelihood-based confidence interval is derived from the asymptotic 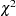 distribution of the generalized likelihood ratio test of Venzon and Moolgavkar (1988). Suppose that the parameter vector is
distribution of the generalized likelihood ratio test of Venzon and Moolgavkar (1988). Suppose that the parameter vector is 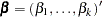 and you want to compute a confidence interval for
and you want to compute a confidence interval for 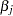 . The profile-likelihood function for
. The profile-likelihood function for 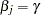 is defined as
is defined as
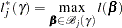 |
where 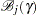 is the set of all
is the set of all 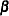 with the
with the 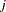 th element fixed at
th element fixed at 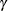 , and
, and  is the log-likelihood function for
is the log-likelihood function for 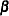 . If
. If 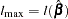 is the log likelihood evaluated at the maximum likelihood estimate
is the log likelihood evaluated at the maximum likelihood estimate 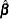 , then
, then 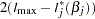 has a limiting chi-square distribution with one degree of freedom if
has a limiting chi-square distribution with one degree of freedom if 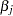 is the true parameter value. Let
is the true parameter value. Let 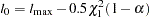 , where
, where 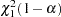 is the
is the 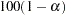 percentile of the chi-square distribution with one degree of freedom. A
percentile of the chi-square distribution with one degree of freedom. A 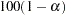 % confidence interval for
% confidence interval for 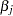 is
is
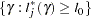 |
The endpoints of the confidence interval are found by solving numerically for values of 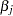 that satisfy equality in the preceding relation. To obtain an iterative algorithm for computing the confidence limits, the log-likelihood function in a neighborhood of
that satisfy equality in the preceding relation. To obtain an iterative algorithm for computing the confidence limits, the log-likelihood function in a neighborhood of 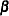 is approximated by the quadratic function
is approximated by the quadratic function
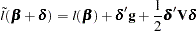 |
where 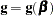 is the gradient vector and
is the gradient vector and 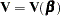 is the Hessian matrix. The increment
is the Hessian matrix. The increment 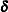 for the next iteration is obtained by solving the likelihood equations
for the next iteration is obtained by solving the likelihood equations
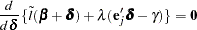 |
where 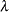 is the Lagrange multiplier,
is the Lagrange multiplier, 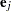 is the
is the 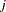 th unit vector, and
th unit vector, and 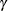 is an unknown constant. The solution is
is an unknown constant. The solution is
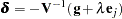 |
By substituting this 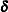 into the equation
into the equation 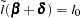 , you can estimate
, you can estimate 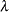 as
as
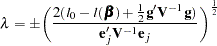 |
The upper confidence limit for 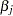 is computed by starting at the maximum likelihood estimate of
is computed by starting at the maximum likelihood estimate of 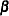 and iterating with positive values of
and iterating with positive values of 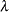 until convergence is attained. The process is repeated for the lower confidence limit, using negative values of
until convergence is attained. The process is repeated for the lower confidence limit, using negative values of 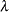 .
.
Convergence is controlled by value  specified with the PLCONV= option in the MODEL statement (the default value of
specified with the PLCONV= option in the MODEL statement (the default value of  is 1E
is 1E 4). Convergence is declared on the current iteration if the following two conditions are satisfied:
4). Convergence is declared on the current iteration if the following two conditions are satisfied:
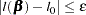 |
and
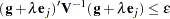 |
The profile-likelihood confidence limits for the hazard ratio 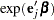 are obtained by exponentiating these confidence limits.
are obtained by exponentiating these confidence limits.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.