| The MI Procedure |
| Descriptive Statistics |
Suppose  is the
is the 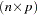 matrix of complete data, which might not be fully observed,
matrix of complete data, which might not be fully observed, 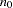 is the number of observations fully observed, and
is the number of observations fully observed, and 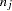 is the number of observations with observed values for variable
is the number of observations with observed values for variable 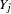 .
.
With complete cases, the sample mean vector is
 |
and the CSSCP matrix is
 |
where each summation is over the fully observed observations.
The sample covariance matrix is
 |
and is an unbiased estimate of the covariance matrix.
The correlation matrix 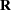 containing the Pearson product-moment correlations of the variables is derived by scaling the corresponding covariance matrix:
containing the Pearson product-moment correlations of the variables is derived by scaling the corresponding covariance matrix:
 |
where  is a diagonal matrix whose diagonal elements are the square roots of the diagonal elements of
is a diagonal matrix whose diagonal elements are the square roots of the diagonal elements of 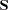 .
.
With available cases, the corrected sum of squares for variable 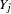 is
is
 |
where  is the sample mean and each summation is over observations with observed values for variable
is the sample mean and each summation is over observations with observed values for variable 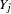 .
.
The variance is
 |
The correlations for available cases contain pairwise correlations for each pair of variables. Each correlation is computed from all observations that have nonmissing values for the corresponding pair of variables.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.