The MDS Procedure

Overview: MDS Procedure

Multidimensional scaling (MDS) refers to a class of methods. These methods estimate coordinates for a set of objects in a space of specified dimensionality. The input data are measurements of distances between pairs of objects. A variety of models can be used that include different ways of computing distances and various functions relating the distances to the actual data. The MDS procedure fits two- and three-way, metric and nonmetric multidimensional scaling models.

The data for the MDS procedure consist of one or more square symmetric or asymmetric matrices of similarities or dissimilarities between objects or stimuli (Kruskal and Wish 1978, pp. 7–11). Such data are also called proximity data. In psychometric applications, each matrix typically corresponds to a subject, and models that fit different parameters for each subject are called individual difference models.

Missing values are permitted. In particular, if the data are all missing except within some off-diagonal rectangle, the analysis is called unfolding. There are, however, many difficulties intrinsic to unfolding models (Heiser; 1981). PROC MDS does not perform external unfolding; for analyses requiring external unfolding, use the TRANSREG procedure instead.

The MDS procedure estimates the following parameters by nonlinear least squares:

configuration	the coordinates of each object in a Euclidean (Kruskal and Wish 1978, pp. 17–19) or weighted Euclidean space (Kruskal and Wish 1978, pp. 61–63) of one or more dimensions
dimension coefficients	for each data matrix, the coefficients that multiply each coordinate of the common or group weighted Euclidean space to yield the individual unweighted Euclidean space. These coefficients are the square roots of the subject weights (Kruskal and Wish 1978, pp. 61–63). A plot of the dimension coefficients is directly interpretable in that it shows how a unit square in the group space is transformed to a rectangle in each individual space. A plot of subject weights has no such simple interpretation. The weighted Euclidean model is related to the INDSCAL model (Carroll and Chang; 1970).
transformation parameters	intercept, slope, or exponent in a linear, affine, or power transformation relating the distances to the data (Kruskal and Wish 1978, pp. 19–22). For a nonmetric analysis, monotone transformations involving no explicit parameters are used (Kruskal and Wish 1978, pp. 22–25). For a discussion of metric versus nonmetric transformations, see Kruskal and Wish (1978, pp. 76–78).

Depending on the LEVEL= option, PROC MDS fits either a regression model of the form

$\text{[math]}$

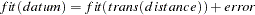or a measurement model of the form

$\text{[math]}$

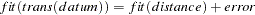where

fit: is a predetermined power or logarithmic transformation specified by the FIT= option.
trans: is an estimated ("optimal") linear, affine, power, or monotone transformation specified by the LEVEL= option.
datum: is a measure of the similarity or dissimilarity of two objects or stimuli.
distance: is a distance computed from the estimated coordinates of the two objects and estimated dimension coefficients in a space of one or more dimensions. If there are no dimension coefficients (COEF=IDENTITY), this is an unweighted Euclidean distance. If dimension coefficients are used (COEF=DIAGONAL), this is a weighted Euclidean distance where the weights are the squares of the dimension coefficients; alternatively, you can multiply each dimension by its coefficient and compute an unweighted Euclidean distance.
error: is an error term assumed to have an approximately normal distribution and to be independently and identically distributed for all data. Under these assumptions, least-squares estimation is statistically appropriate.

For an introduction to multidimensional scaling, see Kruskal and Wish (1978) and Arabie, Carroll, and DeSarbo (1987). A more advanced treatment is given by Young (1987). Many practical issues of data collection and analysis are discussed in Schiffman, Reynolds, and Young (1981). The fundamentals of psychological measurement, including both unidimensional and multidimensional scaling, are expounded by Torgerson (1958). Nonlinear least-squares estimation of PROC MDS models is discussed in Null and Sarle (1982).

Top of Page