For most distributions, the baseline survival function () and the probability density function(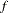) are listed for the additive random disturbance ( or ) with location parameter 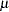and scale parameter . See the section Overview: LIFEREG Procedure for more information. These distributions apply when the log of the response is modeled (this is the default analysis). The corresponding survival function () and its density function () are given for the untransformed baseline distribution ().

For the normal and logistic distributions, the response is not log transformed by PROC LIFEREG, and the survival functions and probability density functions listed apply to the untransformed response.

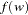For example, for the WEIBULL distribution, and are the survival function and the probability density function for the extreme-value distribution (distribution of the log of the response), while and are the survival function and the probability density function of a Weibull distribution (using the untransformed response).

The chosen baseline functions define the meaning of the intercept, scale, and shape parameters. Only the gamma distribution has a free shape parameter in the following parameterizations. Notice that some of the distributions do not have mean zero and that is not, in general, the standard deviation of the baseline distribution.

For the Weibull distribution, the accelerated failure time model is also a proportional-hazards model. However, the parameterization for the covariates differs by a multiple of the scale parameter from the parameterization commonly used for the proportional hazards model.

The distributions supported in the LIFEREG procedure follow. If there are no covariates in the model, 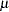= Intercept in the output; otherwise, 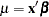. = Scale in the output.

Exponential

where .

Generalized Gamma

, , , , , , and

where denotes the complete gamma function, denotes the incomplete gamma function, and 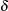is a free shape parameter. The 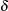parameter is called Shape by PROC LIFEREG. See Lawless (2003, p. 240), and Klein and Moeschberger (1997, p. 386) for a description of the generalized gamma distribution.

Logistic

Loglogistic

where and .

Lognormal

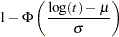where is the cumulative distribution function for the normal distribution.

Normal

where is the cumulative distribution function for the normal distribution.

Weibull

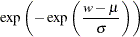where and .

If your parameterization is different from the ones shown here, you can still use the procedure to fit your model. For example, a common parameterization for the Weibull distribution is

so that and .

Again note that the expected value of the baseline log response is, in general, not zero and that the distributions are not symmetric in all cases. Thus, for a given set of covariates, , the expected value of the log response is not always .

Some relations among the distributions are as follows:

• The gamma with Shape=1 is a Weibull distribution.

• The gamma with Shape=0 is a lognormal distribution.

• The Weibull with Scale=1 is an exponential distribution.