| Introduction to Power and Sample Size Analysis |
Equivalence and Noninferiority
Whereas the standard two-sided hypothesis test for a parameter 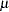 (such as a mean difference) aims to demonstrate that it is significantly different than a null value
(such as a mean difference) aims to demonstrate that it is significantly different than a null value 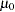 :
:
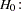 |
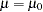 |
|||
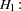 |
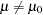 |
an equivalence test instead aims to demonstrate that it is significantly similar to some value, expressed in terms of a range 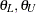 around that value:
around that value:
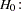 |
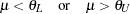 |
|||
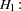 |
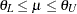 |
Whereas the standard one-sided hypothesis test for 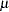 (say, the upper one-sided test) aims to demonstrate that it is significantly greater than
(say, the upper one-sided test) aims to demonstrate that it is significantly greater than 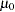 :
:
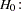 |
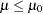 |
|||
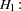 |
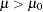 |
a corresponding noninferiority test aims to demonstrate that it is not significantly less than 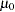 , expressed in terms of a margin
, expressed in terms of a margin 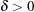 :
:
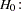 |
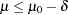 |
|||
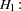 |
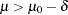 |
Corresponding forms of these hypotheses with the inequalities reversed apply to lower one-sided noninferiority tests (sometimes called nonsuperiority tests).
The POWER procedure performs power analyses for equivalence tests for one-sample, paired, and two-sample tests of normal and lognormal mean differences and ratios. It also supports noninferiority tests for a variety of analyses of means, proportions, and correlation, both directly (with a MARGIN= option representing  ) and indirectly (with an option for a custom null value representing the sum or difference of
) and indirectly (with an option for a custom null value representing the sum or difference of 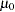 and
and  ).
).
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.