| Introduction to Statistical Modeling with SAS/STAT Software |
Finding the Least Squares Estimators
Finding the least squares estimator of  can be motivated as a calculus problem or by considering the geometry of least squares. The former approach simply states that the OLS estimator is the vector
can be motivated as a calculus problem or by considering the geometry of least squares. The former approach simply states that the OLS estimator is the vector 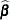 that minimizes the objective function
that minimizes the objective function
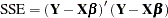 |
Applying the differentiation rules from the section Matrix Differentiation leads to
 |
 |
|||
 |
 |
|||
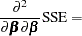 |
 |
Consequently, the solution to the normal equations,  , solves
, solves  , and the fact that the second derivative is nonnegative definite guarantees that this solution minimizes
, and the fact that the second derivative is nonnegative definite guarantees that this solution minimizes  . The geometric argument to motivate ordinary least squares estimation is as follows. Assume that
. The geometric argument to motivate ordinary least squares estimation is as follows. Assume that 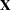 is of rank
is of rank 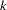 . For any value of
. For any value of  , such as
, such as  , the following identity holds:
, the following identity holds:
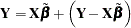 |
The vector 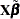 is a point in a
is a point in a 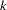 -dimensional subspace of
-dimensional subspace of 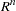 , and the residual
, and the residual  is a point in an
is a point in an  -dimensional subspace. The OLS estimator is the value
-dimensional subspace. The OLS estimator is the value 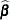 that minimizes the distance of
that minimizes the distance of 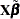 from
from  , implying that
, implying that  and
and 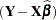 are orthogonal to each other; that is,
are orthogonal to each other; that is,
 . This in turn implies that
. This in turn implies that 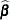 satisfies the normal equations, since
satisfies the normal equations, since
 |
Full-Rank Case
If 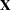 is of full column rank, the OLS estimator is unique and given by
is of full column rank, the OLS estimator is unique and given by
 |
The OLS estimator is an unbiased estimator of  —that is,
—that is,
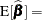 |
 |
|||
 |
 |
Note that this result holds if  ; in other words, the condition that the model errors have mean zero is sufficient for the OLS estimator to be unbiased. If the errors are homoscedastic and uncorrelated, the OLS estimator is indeed the best linear unbiased estimator (BLUE) of
; in other words, the condition that the model errors have mean zero is sufficient for the OLS estimator to be unbiased. If the errors are homoscedastic and uncorrelated, the OLS estimator is indeed the best linear unbiased estimator (BLUE) of  —that is, no other estimator that is a linear function of
—that is, no other estimator that is a linear function of  has a smaller mean squared error. The fact that the estimator is unbiased implies that no other linear estimator has a smaller variance. If, furthermore, the model errors are normally distributed, then the OLS estimator has minimum variance among all unbiased estimators of
has a smaller mean squared error. The fact that the estimator is unbiased implies that no other linear estimator has a smaller variance. If, furthermore, the model errors are normally distributed, then the OLS estimator has minimum variance among all unbiased estimators of  , whether they are linear or not. Such an estimator is called a uniformly minimum variance unbiased estimator, or UMVUE.
, whether they are linear or not. Such an estimator is called a uniformly minimum variance unbiased estimator, or UMVUE.
Rank-Deficient Case
In the case of a rank-deficient 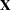 matrix, a generalized inverse is used to solve the normal equations:
matrix, a generalized inverse is used to solve the normal equations:
 |
Although a  -inverse is sufficient to solve a linear system, computational expedience and interpretation of the results often dictate the use of a generalized inverse with reflexive properties (that is, a
-inverse is sufficient to solve a linear system, computational expedience and interpretation of the results often dictate the use of a generalized inverse with reflexive properties (that is, a 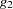 -inverse; see the section Generalized Inverse Matrices for details). Suppose, for example, that the
-inverse; see the section Generalized Inverse Matrices for details). Suppose, for example, that the 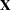 matrix is partitioned as
matrix is partitioned as  , where
, where 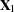 is of full column rank and each column in
is of full column rank and each column in 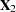 is a linear combination of the columns of
is a linear combination of the columns of 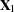 . The matrix
. The matrix
 |
is a  -inverse of
-inverse of 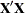 and
and
 |
is a 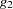 -inverse. If the least squares solution is computed with the
-inverse. If the least squares solution is computed with the  -inverse, then computing the variance of the estimator requires additional matrix operations and storage. On the other hand, the variance of the solution that uses a
-inverse, then computing the variance of the estimator requires additional matrix operations and storage. On the other hand, the variance of the solution that uses a 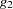 -inverse is proportional to
-inverse is proportional to  .
.
 |
 |
|||
 |
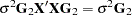 |
If a generalized inverse 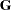 of
of 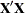 is used to solve the normal equations, then the resulting solution is a biased estimator of
is used to solve the normal equations, then the resulting solution is a biased estimator of  (unless
(unless 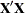 is of full rank, in which case the generalized inverse is "the" inverse), since
is of full rank, in which case the generalized inverse is "the" inverse), since  , which is not in general equal to
, which is not in general equal to  .
.
If you think of estimation as "estimation without bias," then 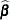 is the estimator of something, namely
is the estimator of something, namely  . Since this is not a quantity of interest and since it is not unique—it depends on your choice of
. Since this is not a quantity of interest and since it is not unique—it depends on your choice of 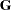 —Searle (1971, p. 169) cautions that in the less-than-full-rank case,
—Searle (1971, p. 169) cautions that in the less-than-full-rank case, 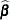 is a solution to the normal equations and "nothing more."
is a solution to the normal equations and "nothing more."
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.