| Introduction to Mixed Modeling Procedures |
| Comparing the MIXED and HPMIXED Procedures |
The experimental HPMIXED procedure is designed to solve large mixed model problems by using sparse matrix techniques. The largeness of a mixed model can take many forms: a large number of observations, large number of columns in the 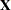 matrix, a large number of random effects, or a large number of covariance parameters. The province of the HPMIXED procedure is parameter estimation, inference, and prediction in mixed models with large
matrix, a large number of random effects, or a large number of covariance parameters. The province of the HPMIXED procedure is parameter estimation, inference, and prediction in mixed models with large 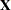 and/or
and/or 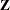 matrices, many observations, but relatively few covariance parameters.
matrices, many observations, but relatively few covariance parameters.
The models that you can fit with the HPMIXED procedure and its postprocessing analyses are a subset of the models and analyses available with the MIXED procedure. With the experimental HPMIXED procedure in SAS 9.2, you can model only G-side random effects with variance component structure or an unstructured covariance matrix in a Cholesky parameterization. R-side random effects and direct modeling of their covariance structures are not supported. A high-performance computing tool has to make concessions with respect to the supported analyses to balance performance and generality.
To some extent, the generality of the MIXED procedure precludes it from serving as a high-performance computing tool for all the model-data scenarios that the procedure can potentially estimate parameters for. For example, although efficient sparse algorithms are available to estimate variance components in large mixed models, the computational configuration changes profoundly when, for example, standard error adjustments and degrees of freedom by the Kenward-Roger method are requested.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.