Dichotomous Response

You have many choices of performing logistic regression in the SAS System. The CATMOD, GENMOD, GLIMMIX, LOGISTIC, PROBIT, and SURVEYLOGISTIC procedures fit the usual logistic regression model.

PROC CATMOD might not be efficient when there are continuous independent variables with large numbers of different values. For a continuous variable with a very limited number of values, PROC CATMOD might still be useful.

PROC GLIMMIX enables you to specify random effects in the models; in particular, you can fit a random-intercept logistic regression model.

PROC LOGISTIC provides the capability of model-building and performs conditional and exact conditional logistic regression. It can also use Firth’s bias-reducing penalized likelihood method.

PROC PROBIT enables you to estimate the natural response rate and compute fiducial limits for the dose variable.

The LOGISTIC, GENMOD, GLIMMIX, PROBIT, and SURVEYLOGISTIC procedures can analyze summarized data by enabling you to input the numbers of events and trials; the ratio of events to trials must be between 0 and 1.

Ordinal Response

PROC LOGISTIC fits the proportional odds model to the ordinal response data by default, PROC PROBIT fits this model if you specify the logistic distribution, and PROC GENMOD and PROC GLIMMIX fit this model if you specify the CLOGIT link and the multinomial distribution. PROC CATMOD fits the cumulative logit or adjacent-category logit response functions.

Nominal Response

When the response variable is nominal, there is no concept of ordering of the response values. Response functions called generalized logits can be fit by the CATMOD, GLIMMIX, and LOGISTIC procedures. PROC CATMOD fits this model by default; PROC GLIMMIX and PROC LOGISTIC require you to specify the GLOGIT link.

Numerical Differences

Differences in the way the models are parameterized and fit might result in different parameter estimates if you perform logistic regression in each of these procedures.

• Parameter estimates from the procedures can differ in sign depending on the ordering of response levels, which you can change if you want.

• The parameter estimates associated with a categorical independent variable might differ among the procedures, since the estimates depend on the coding of the indicator variables in the design matrix. By default, the design matrix column produced by PROC CATMOD and PROC LOGISTIC for a binary independent variable is coded using the values 1 and 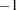(deviation from the mean coding, which is a full-rank parameterization). The same column produced by the CLASS statement of PROC GENMOD, PROC GLIMMIX, and PROC PROBIT is coded using 1 and 0 (GLM coding, which is less-than-full-rank parameterization). As a result, the parameter estimate printed by PROC LOGISTIC is one-half of the estimate produced by PROC GENMOD. Both PROC GENMOD and PROC LOGISTIC allow you to select either a full-rank parameterization or the less-than-full-rank parameterization. The GLIMMIX and PROBIT procedures allow only the less-than-full-rank parameterization for the CLASS variables. The CATMOD procedure allows only full-rank parameterizations. See the "Details" sections in the chapters on the CATMOD, GENMOD, GLIMMIX, LOGISTIC, and PROBIT procedures for more information on the generation of the design matrices used by these procedures. See Chapter 18, Shared Concepts and Topics, for a general discussion of the various parameterizations.

• The maximum-likelihood algorithm used differs among the procedures. PROC LOGISTIC uses the Fisher’s scoring method by default, while PROC PROBIT, PROC GENMOD, PROC GLIMMIX, and PROC CATMOD use the Newton-Raphson method. The parameter estimates should be the same for all three procedures, and the standard errors should be the same for the logistic model. For the normal and extreme-value (Gompertz) distributions in PROC PROBIT, which correspond to the probit and cloglog links, respectively, in PROC GENMOD and PROC LOGISTIC, the standard errors might differ. In general, tests computed using the standard errors from the Newton-Raphson method are more conservative.

• The LOGISTIC, GENMOD, GLIMMIX, and PROBIT procedures can fit a cumulative regression model for ordinal response data by using maximum-likelihood estimation. PROC LOGISTIC and PROC GENMOD use a different parameterization from that of PROC PROBIT, which results in different intercept parameters. Estimates of the slope parameters, however, should be the same for both procedures. The estimated standard errors of the slope estimates are slightly different between the procedures because of the different computational algorithms used as default.