| Introduction to Analysis of Variance Procedures |
Overview: Analysis of Variance Procedures
The statistical term "analyis of variance" is used in a variety of circumstances in statistical theory and applications. In the narrowest sense, and the original sense of the phrase, it signifies a decomposition of a variance into contributing components. This was the sense used by R. A. Fisher when he defined the term to mean the expression of genetic variance as a sum of variance components due to environment, heredity, and so forth:
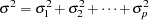 |
In this sense of the term, the SAS/STAT procedures that fit variance component models, such as the GLIMMIX, HPMIXED, MIXED, NESTED, and VARCOMP procedures, are "true" analysis of variance procedures.
Analysis of variance methodology in a slightly broader sense—and the sense most frequently understood today—applies the idea of an additive decomposition of variance to an additive decomposition of sums of squares, whose expected values are functionally related to components of variation. A collection of sums of squares that measure and can be used for inference about meaningful features of a model is called a sum of squares analysis of variance, whether or not such a collection is an additive decomposition. In a linear model, the decomposition of sums of squares can be expressed in terms of projections onto orthogonal subspaces spanned by the columns of the design matrix 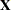 . This is the general approach followed in the section Analysis of Variance in
Chapter 3,
Introduction to Statistical Modeling with SAS/STAT Software.
Depending on the statistical question at hand, the projections can be formulated based on estimable functions, with different types of estimable functions giving rise to different types of sums of squares. Note that not all sum of squares analyses necessarily correspond to additive decompositions. For example, the Type III sums of squares often test hypotheses about the model that are more meaningful than those corresponding to the Type I sums of squares. But while the Type I sums of squares additively decompose the sum of squares due to all model contributions, the Type III sums of squares do not necessarily add up to any useful quantity. The four types of estimable functions in SAS/STAT software, their interpretation, and their construction are discussed in
Chapter 15,
The Four Types of Estimable Functions.
The application of sum of squares analyses is not necessarily limited to models with classification effects (factors). The methodology also applies to linear regression models that contain only continuous regressor variables.
. This is the general approach followed in the section Analysis of Variance in
Chapter 3,
Introduction to Statistical Modeling with SAS/STAT Software.
Depending on the statistical question at hand, the projections can be formulated based on estimable functions, with different types of estimable functions giving rise to different types of sums of squares. Note that not all sum of squares analyses necessarily correspond to additive decompositions. For example, the Type III sums of squares often test hypotheses about the model that are more meaningful than those corresponding to the Type I sums of squares. But while the Type I sums of squares additively decompose the sum of squares due to all model contributions, the Type III sums of squares do not necessarily add up to any useful quantity. The four types of estimable functions in SAS/STAT software, their interpretation, and their construction are discussed in
Chapter 15,
The Four Types of Estimable Functions.
The application of sum of squares analyses is not necessarily limited to models with classification effects (factors). The methodology also applies to linear regression models that contain only continuous regressor variables.
An even broader sense of the term "analysis of variance" pertains to statistical models that contain classification effects (factors), and in particular, to models that contain only classification effects. Any statistical approach that measures features of such a model and can be used for inference is called a general analysis of variance. Thus the procedures for general analysis of variance in SAS/STAT are considered to be those that can fit statistical models containing factors, whether the data are experimental or observational. Some procedures for general analysis of variance have a statistical estimation principle that gives rise to a sum of squares analysis as discussed previously; others express a factor’s contribution to the model fit in some other form. Note that this view of analysis of variance includes, for example, maximum likelihood estimation in generalized linear models with the GENMOD procedure, restricted maximum likelihood estimation in linear mixed models with the MIXED procedure, the estimation of variance components with the VARCOMP procedure, the comparison of means of groups with the TTEST procedure, and the nonparametric analysis of rank scores with the NPAR1WAY procedure, and so on.
In summary, analysis of variance in the contemporary sense of statistical modeling and analysis is more aptly described as analysis of variation, the study of the influences on the variation of a phenomenon. This can take, for example, the following forms:
an analysis of variance table based on sums of squares followed by more specific inquiries into the relationship among factors and their levels
a deviance decomposition in a generalized linear model
a series of Type III tests followed by comparisons of least squares means in a mixed model
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.