Positional and Nonpositional Syntax for Contrast Coefficients

When you define custom linear hypotheses with the CONTRAST or ESTIMATE statement, the GLIMMIX procedure sets up an vector or matrix that conforms to the fixed-effects solutions or the fixed- and random-effects solutions. With the LSMESTIMATE statement, you specify coefficients of the matrix 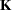that is then converted into a coefficient matrix that conforms to the fixed-effects solutions.

There are two methods for specifying the entries in a coefficient matrix (hereafter simply referred to as the matrix), termed the positional and nonpositional methods. In the positional form, and this is the traditional method, you provide a list of values that occupy the elements of the matrix associated with the effect in question in the order in which the values are listed. For traditional model effects comprising continuous and classification variables, the positional syntax is simpler in some cases (main effects) and more cumbersome in others (interactions). When you work with effects constructed through the experimental EFFECT statement, the nonpositional syntax is essential.

Consider, for example, the following two-way model with interactions where factors A and B have three and two levels, respectively:

   proc glimmix;
      class a b block;
      model y = a b a*b / ddfm=kr;
      random block a*block;
   run;

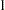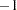To test the difference of the B levels at the second level of A with a CONTRAST statement (a slice), you need to assign coefficients and to the levels of B and to the levels of the interaction where A is at the second level. Two examples of equivalent CONTRAST statements by using positional and nonpositional syntax are as follows:

   contrast 'B at A2' b 1 -1 a*b 0  0  1 -1      ;
   contrast 'B at A2' b 1 -1 a*b [1 2 1] [-1 2 2];

Because A precedes B in the CLASS statement, the levels of the interaction are formed as 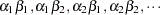. If B precedes A in the CLASS statement, you need to modify the coefficients accordingly:

   proc glimmix;
      class b a block;
      model y = a b a*b / ddfm=kr;
      random block a*block;
      contrast 'B at A2' b 1 -1 a*b 0  1  0  0 -1     ;
      contrast 'B at A2' b 1 -1 a*b [1  1 2] [-1  2 2];
      contrast 'B at A2' b 1 -1 a*b [1, 1 2] [-1, 2 2];
   run;

You can optionally separate the value entry from the level indicators with a comma, as in the last CONTRAST statement.

The general syntax for defining coefficients with the nonpositional syntax is as follows:

The first entry in square brackets is the multiplier that is applied to the elements of for the effect after the level-values have been resolved and any necessary action forming has been taken.

The level-values are organized in a specific form:

• The number of entries should equal the number of terms needed to construct the effect. For effects that do not contain any constructed effects, this number is simply the number of terms in the name of the effect.

• Values of continuous variables needed for the construction of the matrix precede the level indicators of CLASS variables.

• If the effect involves constructed effects, then you need to provide as many continuous and classification variables as are needed for the effect formation. For example, if a grouping effect is defined as

     class c;
     effect v = vars(x1 x2 c);
  

  then a proper nonpositional syntax would be, for example,

     v [0.5,  0.2 0.3 3] 
  

• If an effect contains both regular terms (old-style effects) and constructed effects, then the order of the coefficients is as follows: continuous values for old-style effects, class levels for CLASS variables in old-style effects, continuous values for constructed effects, and finally class levels needed for constructed effects.

  Assume that C has four levels so that effect v contributes six elements to the matrix. When PROC GLIMMIX resolves this syntax, the values 0.2 and 0.3 are assigned to the positions for x1 and x2 and a 1 is associated with the third level of C. The resulting vector is then multiplied by 0.5 to produce

Note that you enter the levels of the classification variables in the square brackets, not their formatted values. The ordering of the levels of CLASS variables can be gleaned from the "Class Level Information" table.

To specify values for continuous variables, simply give their value as one of the terms in the effect. The nonpositional syntax in the following ESTIMATE statement is read as "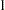-time the value 0.4 in the column associated with level 2 of A"

   proc glimmix;
      class a;
      model y = a a*x / s;
      lsmeans a / e at x=0.4;
      estimate 'A2 at x=0.4' intercept 1 a 0 1 a*x [1,0.4 2] / e;
   run;

Because the value before the comma serves as a multiplier, the same estimable function could also be constructed with the following statements:

   estimate 'A2 at x=0.4' intercept 1 a 0 1 a*x [ 4,  0.1 2];
   estimate 'A2 at x=0.4' intercept 1 a 0 1 a*x [ 2,  0.2 2];
   estimate 'A2 at x=0.4' intercept 1 a 0 1 a*x [-1, -0.4 2];

Note that continuous variables needed to construct an effect are always listed before any CLASS variables.

When you work with constructed effects, the nonpositional syntax works in the same way. For example, the following model contains a classification effect and a B-spline. The first two ESTIMATE statements produce predicted values for level one of C when the continuous variable x takes on the values 20 and 10, respectively.

   proc glimmix;
      class c;
      effect spl = spline(x / knotmethod=equal(5));
      model y = c spl;
      estimate 'C = 1 @ x=20' intercept 1 c 1 spl [1,20],
               'C = 1 @ x=10' intercept 1 c 1 spl [1,10];
      estimate 'Difference'   spl [1,20] [-1,10];
   run;

The GLIMMIX procedure computes the spline coefficients for the first ESTIMATE statement based on 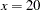, and similarly in the second statement for 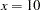. The third ESTIMATE statement computes the difference of the predicted values. Because the spline effect does not interact with the classification variable, this difference does not depend on the level of C. If such an interaction is present, you can estimate the difference in predicted values for a given level of C by using the nonpositional syntax. Because the effect C*spl contains both old-style terms (C) and a constructed effect, you specify the values for the old-style terms before assigning values to constructed effects:

   proc glimmix;
      class c;
      effect spl = spline(x / knotmethod=equal(5));
      model y = spl*c;
      estimate 'C2 = 1, x=20' intercept 1 c*spl [1,1 20];
      estimate 'C2 = 2, x=20' intercept 1 c*spl [1,2 20];
      estimate 'C diff at x=20' c*spl [1,1 20] [-1,2 20];
   run;

It is recommended to add the E option to the CONTRAST, ESTIMATE, or LSMESTIMATE statement to verify that the matrix is formed according to your expectations.

In any row of an ESTIMATE or CONTRAST statement you can choose positional and nonpositional syntax separately for each effect. You cannot mix the two forms of syntax for coefficients of a single effect, however. For example, the following statement is not proper because both forms of syntax are used for the interaction effect:

   estimate 'A1B1 - A1B2' b 1 -1  a*b 0 1  [-1, 1 2];