| The GLIMMIX Procedure |
Design-Adjusted MBN Estimator
Morel (1989) and Morel, Bokossa, and Neerchal (2003) suggested a bias correction of the classical sandwich estimator that rests on an additive correction of the residual crossproducts and a sample size correction. This estimator is available with the EMPIRICAL=MBN option in the PROC GLIMMIX statement. In the notation of the previous section, the residual-based MBN estimator can be written as
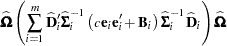 |
where
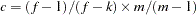 or
or 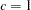 when you specify the EMPIRICAL=MBN(NODF) option
when you specify the EMPIRICAL=MBN(NODF) option  is the sum of the frequencies
is the sum of the frequencies  equals the rank of
equals the rank of 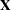
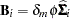
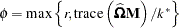
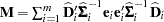
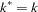 if
if 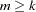 , otherwise
, otherwise 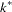 equals the number of nonzero singular values of
equals the number of nonzero singular values of 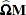
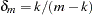 if
if 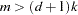 and
and 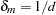 otherwise
otherwise 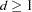 and
and  are parameters supplied with the mbn-options of the EMPIRICAL=MBN(mbn-options) option. The default values are
are parameters supplied with the mbn-options of the EMPIRICAL=MBN(mbn-options) option. The default values are 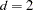 and
and 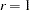 . When the NODF option is in effect, the factor
. When the NODF option is in effect, the factor  is set to 1.
is set to 1.
Rearranging terms, the MBN estimator can also be written as an additive adjustment to a sample-size corrected classical sandwich estimator
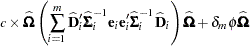 |
Because 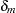 is of order
is of order 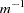 , the additive adjustment to the classical estimator vanishes as the number of independent sampling units (subjects) increases. The parameter
, the additive adjustment to the classical estimator vanishes as the number of independent sampling units (subjects) increases. The parameter 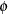 is a measure of the design effect (Morel, Bokossa, and Neerchal 2003). Besides good statistical properties in terms of Type I error rates in small-
is a measure of the design effect (Morel, Bokossa, and Neerchal 2003). Besides good statistical properties in terms of Type I error rates in small-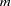 situations, the MBN estimator also has the desirable property of recovering rank when the number of sampling units is small. If
situations, the MBN estimator also has the desirable property of recovering rank when the number of sampling units is small. If 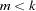 , the "meat" piece of the classical sandwich estimator is essentially a sum of rank one matrices. A small number of subjects relative to the rank of
, the "meat" piece of the classical sandwich estimator is essentially a sum of rank one matrices. A small number of subjects relative to the rank of 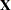 can result in a loss of rank and subsequent loss of numerator degrees of freedom in tests. The additive MBN adjustment counters the rank exhaustion. You can examine the rank of an adjusted covariance matrix with the COVB(DETAILS) option in the MODEL statement.
can result in a loss of rank and subsequent loss of numerator degrees of freedom in tests. The additive MBN adjustment counters the rank exhaustion. You can examine the rank of an adjusted covariance matrix with the COVB(DETAILS) option in the MODEL statement.
When the principle of the MBN estimator is applied to the likelihood-based empirical estimator, you obtain
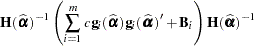 |
where 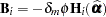 , and
, and 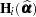 is the second derivative of the log likelihood for the
is the second derivative of the log likelihood for the  th sampling unit (subject) evaluated at the vector of parameter estimates,
th sampling unit (subject) evaluated at the vector of parameter estimates, 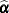 . Also,
. Also, 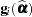 is the first derivative of the log likelihood for the
is the first derivative of the log likelihood for the  th sampling unit. This estimator is computed if you request EMPIRICAL=MBN with METHOD=LAPLACE or METHOD=QUAD.
th sampling unit. This estimator is computed if you request EMPIRICAL=MBN with METHOD=LAPLACE or METHOD=QUAD.
In terms of adjusting the classical likelihood-based estimator (White 1982), the likelihood MBN estimator can be written as
 |
The parameter 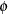 is determined as
is determined as
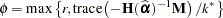
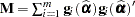
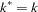 if
if 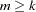 , otherwise
, otherwise 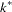 equals the number of nonzero singular values of
equals the number of nonzero singular values of 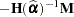
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.