Count data that have an incidence of zero counts greater than expected for the Poisson distribution can be modeled with the zero-inflated Poisson distribution. See Long (1997) and Cameron and Trivedi (1998) for more information about zero-inflated Poisson models. The population is considered to consist of two types of individuals. The first type gives Poisson distributed counts, which might contain zeros. The second type always gives a zero count. Let 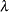be the Poisson mean and 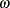be the probability of an individual being of the second type. The parameter 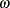is called here the zero-inflation probability, and is the probability of zero counts in excess of the frequency predicted by the Poisson distribution. You can request that the zero inflation probability be displayed in an output data set with the PZERO keyword. The probability distribution of a zero-inflated random variable Y is given by

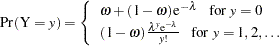You can model the parameters 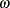and 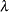in GENMOD with the regression models:

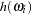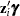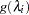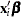where 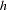is one of the binary link functions: logit, probit, or complementary log-log. The link function 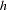is the logit link by default, or the link function option specified in the ZEROMODEL statement. The link function for the Poisson part of the model, , is the log link function by default, or the link function specified in the MODEL statement. The covariates 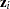for observation are determined by the model specified in the ZEROMODEL statement, and the covariates 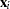are determined by the model specified in the MODEL statement. The regression parameters 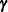and 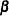are estimated by maximum likelihood.

The mean and variance of Y are given by

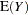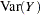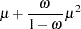You can request that the mean of Y be displayed for each observation in an output data set with the PRED keyword.