The displayed output from PROC DISCRIM includes the class level information table. For each level of the classification variable, the following information is provided: the output data set variable name, frequency sum, weight sum, proportion of the total sample, and prior probability.

The optional output from PROC DISCRIM includes the following:

• Within-class SSCP matrices for each group

• Pooled within-class SSCP matrix

• Between-class SSCP matrix

• Total-sample SSCP matrix

• Within-class covariance matrices, 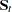, for each group

• Pooled within-class covariance matrix,

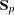
• Between-class covariance matrix, equal to the between-class SSCP matrix divided by 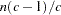, where is the number of observations and is the number of classes

• Total-sample covariance matrix

• Within-class correlation coefficients and to test the hypothesis that the within-class population correlation coefficients are zero

• Pooled within-class correlation coefficients and to test the hypothesis that the partial population correlation coefficients are zero

• Between-class correlation coefficients and to test the hypothesis that the between-class population correlation coefficients are zero

• Total-sample correlation coefficients and to test the hypothesis that the total population correlation coefficients are zero

• Simple statistics, including 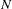(the number of observations), sum, mean, variance, and standard deviation both for the total sample and within each class

• Total-sample standardized class means, obtained by subtracting the grand mean from each class mean and dividing by the total-sample standard deviation

• Pooled within-class standardized class means, obtained by subtracting the grand mean from each class mean and dividing by the pooled within-class standard deviation

• Pairwise squared distances between groups

• Univariate test statistics, including total-sample standard deviations, pooled within-class standard deviations, between-class standard deviations, R square, , , 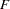and 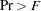(univariate 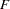values and probability levels for one-way analyses of variance)

• Multivariate statistics and 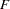approximations, including Wilks’ lambda, Pillai’s trace, Hotelling-Lawley trace, and Roy’s greatest root with 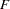approximations, numerator and denominator degrees of freedom (Num DF and Den DF), and probability values 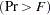. Each of these four multivariate statistics tests the hypothesis that the class means are equal in the population. See the section Multivariate Tests in Chapter 4, Introduction to Regression Procedures, for more information.

If you specify METHOD=NORMAL, the following three statistics are displayed:

• Covariance matrix information, including covariance matrix rank and natural log of determinant of the covariance matrix for each group (POOL=TEST, POOL=NO) and for the pooled within-group (POOL=TEST, POOL=YES)

• Optionally, test of homogeneity of within covariance matrices (the results of a chi-square test of homogeneity of the within-group covariance matrices) (Morrison; 1976; Kendall, Stuart, and Ord; 1983; Anderson; 1984)

• Pairwise generalized squared distances between groups

If the CANONICAL option is specified, the displayed output contains these statistics:

• Canonical correlations

• Adjusted canonical correlations (Lawley; 1959). These are asymptotically less biased than the raw correlations and can be negative. The adjusted canonical correlations might not be computable and are displayed as missing values if two canonical correlations are nearly equal or if some are close to zero. A missing value is also displayed if an adjusted canonical correlation is larger than a previous adjusted canonical correlation.

• Approximate standard error of the canonical correlations

• Squared canonical correlations

• Eigenvalues of 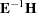. Each eigenvalue is equal to 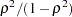, where 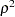is the corresponding squared canonical correlation and can be interpreted as the ratio of between-class variation to within-class variation for the corresponding canonical variable. The table includes eigenvalues, differences between successive eigenvalues, proportion of the sum of the eigenvalues, and cumulative proportion.

• Likelihood ratio for the hypothesis that the current canonical correlation and all smaller ones are zero in the population. The likelihood ratio for all canonical correlations equals Wilks’ lambda.

• Approximate 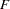statistic based on Rao’s approximation to the distribution of the likelihood ratio (Rao 1973, p. 556; Kshirsagar 1972, p. 326)

• Numerator degrees of freedom (Num DF), denominator degrees of freedom (Den DF), and 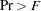, the probability level associated with the 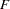statistic

The following statistic concerns the classification criterion:

• the linear discriminant function, but only if you specify METHOD=NORMAL and the pooled covariance matrix is used to calculate the (generalized) squared distances

When the input DATA= data set is an ordinary SAS data set, the displayed output includes the following:

• Optionally, the resubstitution results including the observation number (if an ID statement is included, the values of the ID variable are displayed instead of the observation number), the actual group for the observation, the group into which the developed criterion would classify it, and the posterior probability of membership in each group

• Resubstitution summary, a summary of the performance of the classification criterion based on resubstitution classification results

• Error count estimate of the resubstitution classification results

• Optionally, posterior probability error rate estimates of the resubstitution classification results

If you specify the CROSSVALIDATE option, the displayed output contains these statistics:

• Optionally, the cross validation results including the observation number (if an ID statement is included, the values of the ID variable are displayed instead of the observation number), the actual group for the observation, the group into which the developed criterion would classify it, and the posterior probability of membership in each group

• Cross validation summary, a summary of the performance of the classification criterion based on cross validation classification results

• Error count estimate of the cross validation classification results

• Optionally, posterior probability error rate estimates of the cross validation classification results

If you specify the TESTDATA= option, the displayed output contains these statistics:

• Optionally, the classification results including the observation number (if a TESTID statement is included, the values of the ID variable are displayed instead of the observation number), the actual group for the observation (if a TESTCLASS statement is included), the group into which the developed criterion would classify it, and the posterior probability of membership in each group

• Classification summary, a summary of the performance of the classification criterion

• Error count estimate of the test data classification results

• Optionally, posterior probability error rate estimates of the test data classification results