General Formulas

Canonical discriminant analysis is equivalent to canonical correlation analysis between the quantitative variables and a set of dummy variables coded from the class variable. In the following notation the dummy variables are denoted by 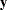and the quantitative variables by . The total sample covariance matrix for the and 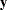variables is

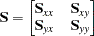When is the number of groups, is the number of observations in group , and 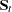is the sample covariance matrix for the variables in group , the within-class pooled covariance matrix for the variables is

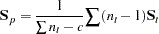The canonical correlations, 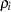, are the square roots of the eigenvalues, 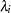, of the following matrix. The corresponding eigenvectors are .

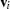Let 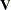be the matrix with the eigenvectors 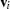that correspond to nonzero eigenvalues as columns. The raw canonical coefficients are calculated as follows:

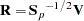The pooled within-class standardized canonical coefficients are

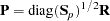The total sample standardized canonical coefficients are

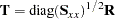Let 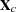be the matrix with the centered variables as columns. The canonical scores can be calculated by any of the following:

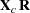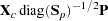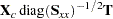For the multivariate tests based on ,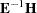

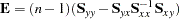where is the total number of observations.