OUT= Data Set

The OUT= data set contains all the variables in the original data set plus new variables containing the canonical variable scores. The number of new variables is twice that specified by the NCAN= option. The names of the new variables are formed by concatenating the values given by the VPREFIX= and WPREFIX= options (the defaults are V and W) with the numbers 1, 2, 3, and so on. The new variables have mean 0 and variance equal to 1. An OUT= data set cannot be created if the DATA= data set is TYPE=CORR, COV, FACTOR, SSCP, UCORR, or UCOV.

If you use a PARTIAL statement, the OUT= data set also contains the residuals from predicting the VAR variables from the PARTIAL variables. The names of the residual variables are formed by concatenating the values given by the PARPREFIX= option (the default is R_) with the numbers 1, 2, 3, and so on.

OUTSTAT= Data Set

The OUTSTAT= data set is similar to the TYPE=CORR or TYPE=UCORR data set produced by the CORR procedure, but it contains several results in addition to those produced by PROC CORR.

The new data set contains the following variables:

• the BY variables, if any

• two new character variables, _TYPE_ and _NAME_

• Intercept, if the INT option is used

• the variables analyzed (those in the VAR statement and the WITH statement)

Each observation in the new data set contains some type of statistic as indicated by the _TYPE_ variable. The values of the _TYPE_ variable are as follows.

_TYPE_

MEAN

means

STD

standard deviations

USTD

uncorrected standard deviations. When you specify the NOINT option in the PROC CANCORR statement, the OUTSTAT= data set contains standard deviations not corrected for the mean (_TYPE_=’USTD’).

N

number of observations on which the analysis is based. This value is the same for each variable.

SUMWGT

sum of the weights if a WEIGHT statement is used. This value is the same for each variable.

CORR

correlations. The _NAME_ variable contains the name of the variable corresponding to each row of the correlation matrix.

UCORR

uncorrected correlation matrix. When you specify the NOINT option in the PROC CANCORR statement, the OUTSTAT= data set contains a matrix of correlations not corrected for the means.

CORRB

correlations among the regression coefficient estimates

STB

standardized regression coefficients. The _NAME_ variable contains the name of the dependent variable.

B

raw regression coefficients

SEB

standard errors of the regression coefficients

LCLB

95% lower confidence limits for the regression coefficients

UCLB

95% upper confidence limits for the regression coefficients

T

statistics for the regression coefficients

PROBT

probability levels for the statistics

SPCORR

semipartial correlations between regressors and dependent variables

SQSPCORR

squared semipartial correlations between regressors and dependent variables

PCORR

partial correlations between regressors and dependent variables

SQPCORR

squared partial correlations between regressors and dependent variables

RSQUARED

R squares for the multiple regression analyses

ADJRSQ

adjusted R squares

LCLRSQ

approximate 95% lower confidence limits for the R squares

UCLRSQ

approximate 95% upper confidence limits for the R squares

F

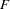statistics for the multiple regression analyses

PROBF

probability levels for the 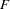statistics

CANCORR

canonical correlations

SCORE

standardized canonical coefficients. The _NAME_ variable contains the name of the canonical variable.

To obtain the canonical variable scores, these coefficients should be multiplied by the standardized data, using means obtained from the observation with _TYPE_=’MEAN’ and standard deviations obtained from the observation with _TYPE_=’STD’.

RAWSCORE

raw canonical coefficients.

To obtain the canonical variable scores, these coefficients should be multiplied by the raw data centered by means obtained from the observation with _TYPE_=’MEAN’.

USCORE

scoring coefficients to be applied without subtracting the mean from the raw variables. These are standardized canonical coefficients computed under a NOINT model.

To obtain the canonical variable scores, these coefficients should be multiplied by the data that are standardized by the uncorrected standard deviations obtained from the observation with _TYPE_=’USTD’.

STRUCTUR

canonical structure.