Shared Statistical Concepts

Adaptive Lasso Selection

Adaptive lasso selection is a modification of lasso selection; in adaptive lasso selection, weights are applied to each of the parameters in forming the lasso constraint (Zou 2006). More precisely, suppose that the response y has mean 0 and the regressors x are scaled to have mean 0 and common standard deviation. Furthermore, suppose that you can find a suitable estimator 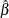$\hat\beta$ of the parameters in the true model and you define a weight vector by 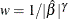$w=1/| \hat\beta |^\gamma$ , where 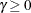$\gamma \geq 0$ . Then the adaptive lasso regression coefficients 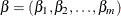$\beta = (\beta _1,\beta _2,\ldots ,\beta _ m)$ are the solution to the following constrained optimization problem:

$\mbox{minimize} ||\mb{y}-\bX \bbeta ||^2 \qquad \mbox{subject to} \quad \sum _{j=1}^{m} | w_ j\beta _ j | \leq t$

PROC HPREG uses the solution to the unconstrained least squares problem as the estimator 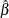$\hat\beta$ . This is appropriate unless collinearity is a concern. If the regressors are collinear or nearly collinear, then Zou (2006) suggests using a ridge regression estimate to form the adaptive weights.