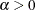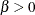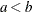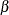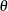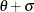Random Variation in a Model

Beta

The density function of the beta distribution is

\[ f(x) = \frac{\Gamma (\alpha + \beta )}{\Gamma (\alpha )\Gamma (\beta )(b - a)^{\alpha + \beta - 1}}(x - a)^{\alpha - 1}(b - x)^{\beta - 1} \]

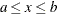for $a \le x \le b$. The gamma function 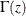$\Gamma (z)$ is defined for any real number 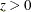$z > 0$ as

\[ \Gamma (z) = \int _{0}^{\infty }t^{z - 1}e^{-t}dt \]

Parameters:

$\alpha > 0$

is a shape parameter.

$\beta > 0$

is a shape parameter.

a

is the minimum value, $a < b$.

b

is the maximum value.

Table B.6 shows how the beta distribution parameter names are specified in Simulation Studio (specifically, in the Numeric Source block) and in JMP.

Table B.6: Beta Distribution Parameter Names

 

Simulation Studio

JMP

$\alpha $

Shape 1

$\alpha $

$\beta $

Shape 2

$\beta $

a

Min

$\theta $

b

Max

$\theta + \sigma $


The following examples show (case-sensitive) string values that can be used as Numeric Source block DataStreamDescription factor values or InStreamPolicy port values. In these examples, the distribution and parameter names in the string value are the names that are used in the Theoretical option in the Numeric Source Block Properties dialog box (including any spaces or hyphens). Quotation marks are not required around the string value, and you can specify only the parameters that need to be updated (as demonstrated in the second example).

  • class == Beta;Min == 0;Max == 1;Shape 2 = 5;Shape 1 == 1.5

  • Shape 1 == 5;Shape 2 == 1.5