Random Variation in a Model
The Empirical option under the Data Driven option of a Numeric Source block requires the following input data:
-
Data Name: The location of the SAS data set or JMP table that contains the data to be used to specify a continuous empirical distribution.
-
X : Name of the column in the data set that corresponds to the set of n ordered values
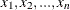 .
.
-
C : Name of the column in the data set that corresponds to the cumulative probability values
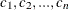 so that
so that 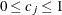 for
for 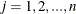 ;
; 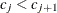 for
for 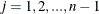 ; and
; and 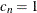 .
.
The probability density function is defined as
![\[ f(x) = \left\{ \begin{array}{ll} c_1 & \mbox{if } x=x_1 \\ c_ j - c_{j-1} & \mbox{if } x_{j-1} \leq x < x_ j, j=2,3,...,n \\ 0 & \mbox{if } x < x_1 \ \mbox{or } x \geq x_ n \end{array} \right. \]](images/simsug_app20087.png)
If ![]() , then the result is a mixed continuous-discrete distribution that returns
, then the result is a mixed continuous-discrete distribution that returns ![]() with probability
with probability ![]() and with probability
and with probability ![]() a continuous random variate on
a continuous random variate on ![]() using linear interpolation. If a true continuous distribution on
using linear interpolation. If a true continuous distribution on ![]() is desired, then specify
is desired, then specify ![]() .
.